Page 129 - Fundamentals of Computational Geoscience Numerical Methods and Algorithms

5.3 Application of the Segregated Algorithm 117

τ
τ
(Numerical, = . 0 03) (Numerical, = . 0 04)

τ
τ
(Numerical, = . 0 05) (Numerical, = . 0 06)

τ
(Numerical, = . 0 07 (Numerical, τ = . 0 08)
)
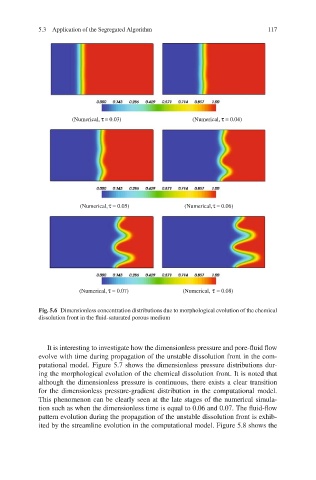
Fig. 5.6 Dimensionless concentration distributions due to morphological evolution of the chemical
dissolution front in the fluid-saturated porous medium

It is interesting to investigate how the dimensionless pressure and pore-fluid flow
evolve with time during propagation of the unstable dissolution front in the com-
putational model. Figure 5.7 shows the dimensionless pressure distributions dur-
ing the morphological evolution of the chemical dissolution front. It is noted that
although the dimensionless pressure is continuous, there exists a clear transition
for the dimensionless pressure-gradient distribution in the computational model.
This phenomenon can be clearly seen at the late stages of the numerical simula-
tion such as when the dimensionless time is equal to 0.06 and 0.07. The fluid-flow
pattern evolution during the propagation of the unstable dissolution front is exhib-
ited by the streamline evolution in the computational model. Figure 5.8 shows the