Page 37 - Fundamentals of Computational Geoscience Numerical Methods and Algorithms

2.6 Application of the Progressive Asymptotic Approach Procedure 23

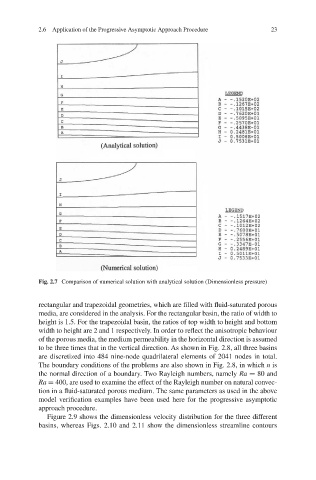
Fig. 2.7 Comparison of numerical solution with analytical solution (Dimensionless pressure)

rectangular and trapezoidal geometries, which are filled with fluid-saturated porous
media, are considered in the analysis. For the rectangular basin, the ratio of width to
height is 1.5. For the trapezoidal basin, the ratios of top width to height and bottom
width to height are 2 and 1 respectively. In order to reflect the anisotropic behaviour
of the porous media, the medium permeability in the horizontal direction is assumed
to be three times that in the vertical direction. As shown in Fig. 2.8, all three basins
are discretized into 484 nine-node quadrilateral elements of 2041 nodes in total.
The boundary conditions of the problems are also shown in Fig. 2.8, in which n is
the normal direction of a boundary. Two Rayleigh numbers, namely Ra = 80 and
Ra = 400, are used to examine the effect of the Rayleigh number on natural convec-
tion in a fluid-saturated porous medium. The same parameters as used in the above
model verification examples have been used here for the progressive asymptotic
approach procedure.
Figure 2.9 shows the dimensionless velocity distribution for the three different
basins, whereas Figs. 2.10 and 2.11 show the dimensionless streamline contours