Page 33 - Fundamentals of Computational Geoscience Numerical Methods and Algorithms

2.5 Verification of the Proposed Progressive Asymptotic Approach 19

mπ

∗
∗
u = nπC 1 sin x ∗ cos(nπy ), (2.63)
L ∗
mπ mπ
∗ ∗ ∗
v =− C 1 cos x sin(nπy ), (2.64)
L ∗ L ∗
mπ
C 1
∗ ∗ ∗ ∗
T =−√ cos x sin(nπy ) + (1 − y ), (2.65)
Ra critical L ∗
nL ∗ mπ Ra critical
∗ ∗ ∗ ∗ 2
P = C 1 cos x cos(nπy ) − (1 − y ) + C 2 , (2.66)
m L ∗ 2
where the values of m, n and Ra critical are dependent on whether L is an integer
∗
or not; C 1 is a non-zero constant and C 2 is an arbitrary constant. It is interesting
to note that since Ra critical is a function of L , it can vary with a non-integer L .
∗
∗
This implies that if rectangular valleys are filled with porous media, they may have
different critical Rayleigh numbers when their ratios of length to height are different.

2.5 Verification of the Proposed Progressive Asymptotic
Approach Procedure Associated with Finite
Element Analysis

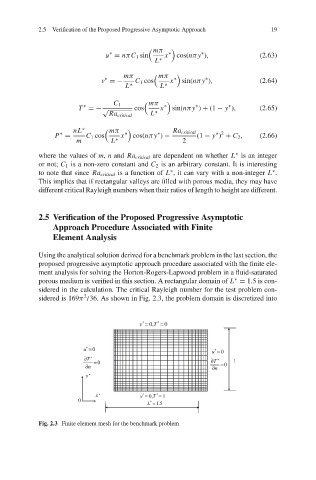
Using the analytical solution derived for a benchmark problem in the last section, the
proposed progressive asymptotic approach procedure associated with the finite ele-
ment analysis for solving the Horton-Rogers-Lapwood problem in a fluid-saturated
∗
porous medium is verified in this section. A rectangular domain of L = 1.5 is con-
sidered in the calculation. The critical Rayleigh number for the test problem con-
2
sidered is 169π /36. As shown in Fig. 2.3, the problem domain is discretized into

*
*
v = 0,T = 0
*
u = 0
*
u = 0
∂T *
= 0 ∂T * 1
∂n ∂n = 0
* y
* x * *
v = 0,T = 1
0 *
L = 1.5
Fig. 2.3 Finite element mesh for the benchmark problem