Page 135 - Fundamentals of Magnetic Thermonuclear Reactor Design

Superconducting Magnet Systems Chapter | 5 119

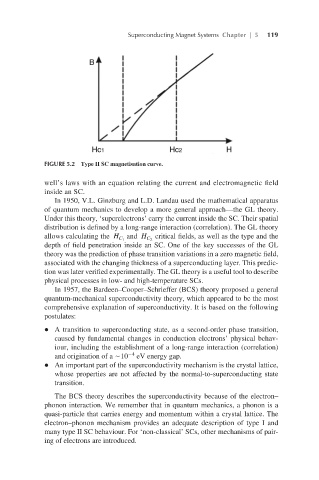
FIGURE 5.2 Type II SC magnetisation curve.

well’s laws with an equation relating the current and electromagnetic field
inside an SC.
In 1950, V.L. Ginzburg and L.D. Landau used the mathematical apparatus
of quantum mechanics to develop a more general approach—the GL theory.
Under this theory, ‘superelectrons’ carry the current inside the SC. Their spatial
distribution is defined by a long-range interaction (correlation). The GL theory
allows calculating the H and H critical fields, as well as the type and the HC 1
C 1
C 2
depth of field penetration inside an SC. One of the key successes of the GL
theory was the prediction of phase transition variations in a zero magnetic field,
associated with the changing thickness of a superconducting layer. This predic-
tion was later verified experimentally. The GL theory is a useful tool to describe
physical processes in low- and high-temperature SCs.
In 1957, the Bardeen–Cooper–Schrieffer (BCS) theory proposed a general
quantum-mechanical superconductivity theory, which appeared to be the most HC 2
comprehensive explanation of superconductivity. It is based on the following
postulates:
l A transition to superconducting state, as a second-order phase transition,
caused by fundamental changes in conduction electrons’ physical behav-
iour, including the establishment of a long-range interaction (correlation)
−4
and origination of a ∼10 eV energy gap.
l An important part of the superconductivity mechanism is the crystal lattice,
whose properties are not affected by the normal-to-superconducting state
transition.
The BCS theory describes the superconductivity because of the electron–
phonon interaction. We remember that in quantum mechanics, a phonon is a
quasi-particle that carries energy and momentum within a crystal lattice. The
electron–phonon mechanism provides an adequate description of type I and
many type II SC behaviour. For ‘non-classical’ SCs, other mechanisms of pair-
ing of electrons are introduced.