Page 73 - Fundamentals of Ocean Renewable Energy Generating Electricity From The Sea

Tidal Energy Chapter | 3 65

The solution of Eq. (3.24) can be based on a simple harmonic wave (i.e. M2
tidal signal)
η t = a M2 cos (ω M2 t − φ) (3.25)
or combination of two or more astronomical components (e.g. M2 and S2),
depending on the forcing at the boundary of the domain. However, the solution
of Eq. (3.23) cannot be only based on the M2 signal, due to the presence of
nonlinear terms. As we know from Fourier analysis, any function, regardless
of complexity, can be reconstructed by harmonic components if we add other
higher-frequency terms. In other words, the solution of Eq. (3.23) can be based
on a series like this

η t = [a M2 cos (ω M2 t − φ)] astronomical tide
+ ··· + [a 2 cos (2ω M2 t − φ 2 ) + a 3 cos (3ω M2 t − φ 3 )
+a 4 cos (4ω M2 t − φ 2 ) + ··· ] overtide (3.26)

The additional terms, which appear in the previous equation, are called
overtides. In particular, M4 is the second term, with a frequency of 2ω M2 ,M6
has a frequency of 3ω M2 , M8 has the frequency of 4ω M2 , and so on.
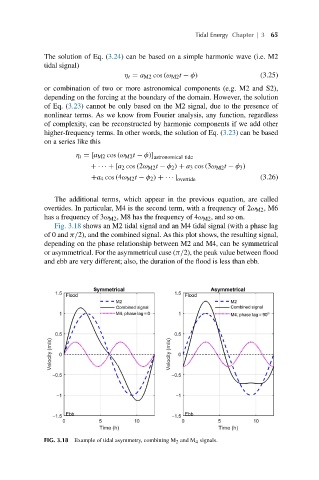
Fig. 3.18 shows an M2 tidal signal and an M4 tidal signal (with a phase lag
of 0 and π/2), and the combined signal. As this plot shows, the resulting signal,
depending on the phase relationship between M2 and M4, can be symmetrical
or asymmetrical. For the asymmetrical case (π/2), the peak value between flood
and ebb are very different; also, the duration of the flood is less than ebb.

FIG. 3.18 Example of tidal asymmetry, combining M 2 and M 4 signals.