Page 75 - Fundamentals of Ocean Renewable Energy Generating Electricity From The Sea

Tidal Energy Chapter | 3 67

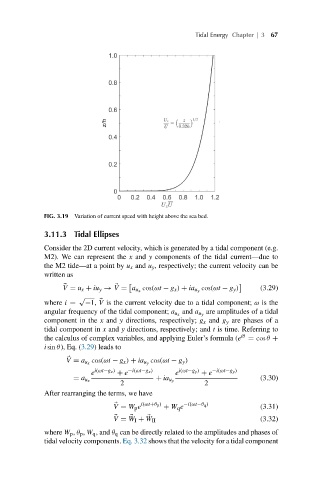
FIG. 3.19 Variation of current speed with height above the sea bed.

3.11.3 Tidal Ellipses
Consider the 2D current velocity, which is generated by a tidal component (e.g.
M2). We can represent the x and y components of the tidal current—due to
the M2 tide—at a point by u x and u y , respectively; the current velocity can be
written as

cos(ωt − g y ) (3.29)
V = u x + iu y → V = a u x
cos(ωt − g x ) + ia u y
√
where i = −1, V is the current velocity due to a tidal component; ω is the
are amplitudes of a tidal
angular frequency of the tidal component; a u x and a u y
component in the x and y directions, respectively; g x and g y are phases of a
tidal component in x and y directions, respectively; and t is time. Referring to
iθ
the calculus of complex variables, and applying Euler’s formula (e = cos θ +
i sin θ), Eq. (3.29) leads to
cos(ωt − g y )
V = a u x
cos(ωt − g x ) + ia u y
e i(ωt−g x ) + e −i(ωt−g x ) e i(ωt−g y ) + e −i(ωt−g y )
(3.30)
= a u x + ia u y
2 2
After rearranging the terms, we have
V = W p e i(ωt+θ p ) + W q e −i(ωt−θ q ) (3.31)
V = W I + W II (3.32)
where W p , θ p , W q , and θ q can be directly related to the amplitudes and phases of
tidal velocity components. Eq. 3.32 shows that the velocity for a tidal component