Page 237 - Fundamentals of Probability and Statistics for Engineers

220 Fundamentals of Probability and Statistics for Engineers

The parameter n is generally referred to as the degrees of freedom. The utility of
this distribution arises from the fact that a sum of the squares of n independent
standardized normal random variables has a 2 distribution with n degrees of
freedom; that is, if U 1 , U 2 ,..., and U n are independent and distributed as
N(0, 1), the sum

2
2
X ˆ U ‡ U ‡ ‡ U n 2 7:68†
2
1
has a 2 distribution with n degrees of freedom. One can verify this statement
2
by determining the characteristic function of each U (see Example 5.7, page
j
132) and using the method of characteristic functions as discussed in Section 4.5
for sums of independent random variables.
Because of this relationship, the 2 distribution is one of our main tools in
the area of statistical inference and hypothesis testing. These applications are
detailed in Chapter 10.

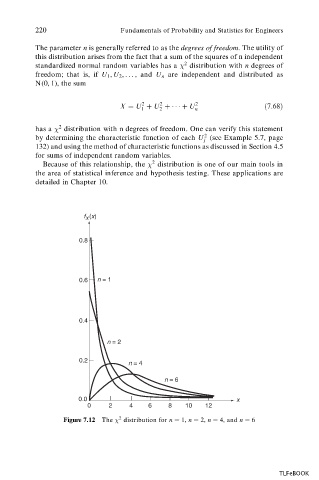
f (x)
X

0.8

0.6 n = 1

0.4

n = 2

0.2
n = 4

n = 6

0.0 x
0 2 4 6 8 10 12
Figure 7.12 The 2 distribution for n ˆ 1, n ˆ 2, n ˆ 4, and n ˆ 6

TLFeBOOK