Page 304 - Fundamentals of Probability and Statistics for Engineers

Parameter Estimation 287

1

Θ ∗ 2 Θ ∗ 3

Θ ∧ (1)
Asymptotic efficiency 0.1 Θ
∧ (2)

Θ ∧ (3)

0.01
0.01 0.1 1
θ
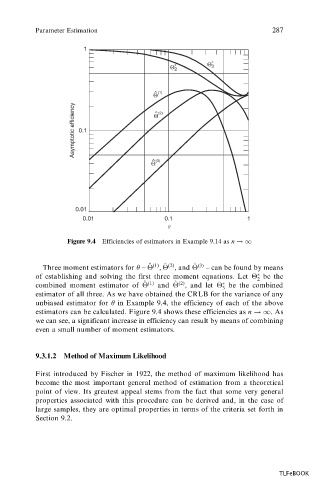
Figure 9.4 Efficiencies of estimators in Example 9.14 as n !1

^
^ 1) ^ 2)
Three moment estimators for ± , ,and (3) – can be found by means
of establishing and solving the first three moment equations. Let 2 be the
^
^
combined moment estimator of (1) and (2) ,and let be the combined
3
estimator of all three. As we have obtained the CRLB for the variance of any
unbiased estimator for in Example 9.4, the efficiency of each of the above
estimators can be calculated. Figure 9.4 shows these efficiencies as n !1
. As
we can see, a significant increase in efficiency can result by means of combining
even a small number of moment estimators.

9.3.1.2 Method of Maximum Likelihood

First introduced by Fischer in 1922, the method of maximum likelihood has
become the most important general method of estimation from a theoretical
point of view. Its greatest appeal stems from the fact that some very general
properties associated with this procedure can be derived and, in the case of
large samples, they are optimal properties in terms of the criteria set forth in
Section 9.2.

TLFeBOOK