Page 309 - Fundamentals of Probability and Statistics for Engineers

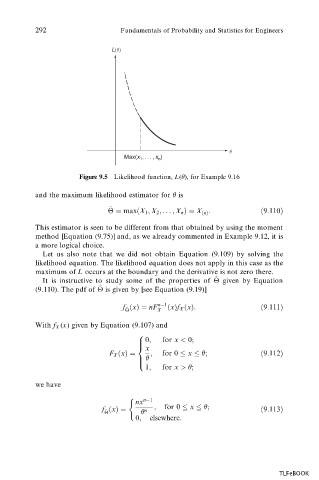
292 Fundamentals of Probability and Statistics for Engineers

L(θ)

θ
Max(x 1 ,..., x n )

Figure 9.5 Likelihood function, L( ), for Example 9.16

and the maximum likelihood estimator for is
^
ˆ max X 1 ; X 2 ; ... ; X n †ˆ X n† : 9:110†
This estimator is seen to be different from that obtained by using the moment
method [Equation (9.75)] and, as we already commented in Example 9.12, it is
a more logical choice.
Let us also note that we did not obtain Equation (9.109) by solving the
likelihood equation. The likelihood equation does not apply in this case as the
maximum of L occurs at the boundary and the derivative is not zero there.
^
It is instructive to study some of the properties of given by Equation
^
(9.110). The pdf of is given by [see Equation (9.19)]
x†ˆ nF n 1 x†f X x†: 9:111†
X
f ^
With f X (x) given by Equation (9.107) and

8
0; for x < 0;
>
>
x
<
F X x†ˆ ; for 0 x ; 9:112†

>
>
1; for x > ;
:
we have
n 1
nx
x†ˆ n ; for 0 x ; 9:113†
f ^
0; elsewhere:

TLFeBOOK