Page 354 - Fundamentals of Probability and Statistics for Engineers

Linear Models and Linear Regression 337

y

(x ,y ) i
i
Estimated regression line:
∧ ∧
e i y = α + βx

True regression line:
y = α + βx

x

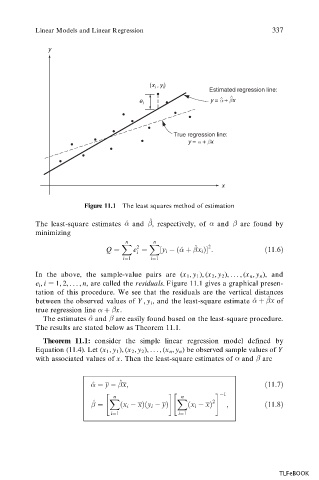
Figure 11.1 The least squares method of estimation

The least-square estimates ^ and ^ , respectively, of and are found by
minimizing
n n
^
X 2 X 2
Q ˆ e ˆ ‰y i ^ ‡ x i †Š : 11:6†
i
iˆ1 iˆ1
In the above, the sample-value pairs are (x 1 , y 1 ), (x 2 , y 2 ), . . . , (x n , y n ), and
e i , i ˆ 1, 2, ..., n, are called the residuals. Figure 11.1 gives a graphical presen-
tation of this procedure. We see that the residuals are the vertical distances
^
between the observed values of Y , y i , and the least-square estimate ^ ‡ x of
true regression line ‡ x.
The estimates ^ and are easily found based on the least-square procedure.
The results are stated below as Theorem 11.1.
Theorem 11.1: consider the simple linear regression model defined by
Equation (11.4). Let (x 1 , y 1 ), (x 2 , y 2 ), . . ., (x n , y n ) be observed sample values of Y
with associated values of x. Then the least-square estimates of and are

^
^ ˆ y x; 11:7†
" #" # 1
n X
n
^
X
ˆ x i x† y i y† x i x† 2 ; 11:8†
iˆ1 iˆ1

TLFeBOOK