Page 59 - Fundamentals of Probability and Statistics for Engineers

42 Fundamentals of Probability and Statistics for Engineers

p (x)
X

1
2

1
8
x
–2 –1 0 1 2 3 4
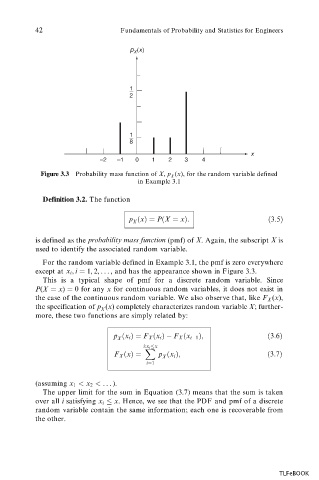
Figure 3.3 Probability mass function of X, p 9x), for the random variable defined
X
in Example 3.1
Definition 3.2. The function

p x†ˆ P X ˆ x†: 3:5†
X

is defined as the probability mass function (pmf) of X . Again, the subscript X is
used to identify the associated random variable.
For the random variable defined in Example 3.1, the pmf is zero everywhere
except at x i , i ˆ 1, 2, . . . , and has the appearance shown in Figure 3.3.
This is a typical shape of pmf for a discrete random variable. Since
P9X ˆ x) ˆ 0 for any x for continuous random variables, it does not exist in
the case of the continuous random variable. We also observe that, like F X 9x),
X
the specification of p 9x) completely characterizes random variable ; further-
X
more, these two functions are simply related by:
p x i †ˆ F X x i † F X x i 1 †; 3:6†
X
i:x i x
X
F X x†ˆ p x i †; 3:7†
X
iˆ1
(assuming x 1 < x 2 < . . . ).
The upper limit for the sum in Equation (3.7) means that the sum is taken
over all satisfying x i x. Hence, we see that the PDF and pmf of a discrete
i
random variable contain the same information; each one is recoverable from
the other.

TLFeBOOK