Page 183 - Fundamentals of Radar Signal Processing

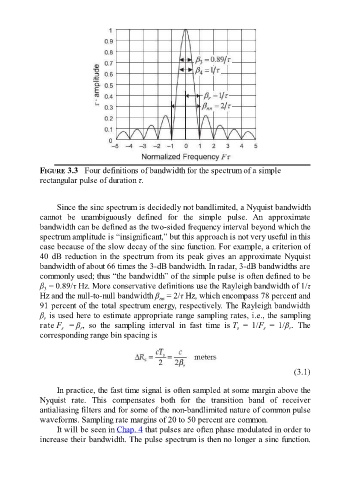
FIGURE 3.3 Four definitions of bandwidth for the spectrum of a simple
rectangular pulse of duration τ.

Since the sinc spectrum is decidedly not bandlimited, a Nyquist bandwidth
cannot be unambiguously defined for the simple pulse. An approximate
bandwidth can be defined as the two-sided frequency interval beyond which the
spectrum amplitude is “insignificant,” but this approach is not very useful in this
case because of the slow decay of the sinc function. For example, a criterion of

40 dB reduction in the spectrum from its peak gives an approximate Nyquist
bandwidth of about 66 times the 3-dB bandwidth. In radar, 3-dB bandwidths are
commonly used; thus “the bandwidth” of the simple pulse is often defined to be
β = 0.89/τ Hz. More conservative definitions use the Rayleigh bandwidth of 1/τ
3
Hz and the null-to-null bandwidth β = 2/τ Hz, which encompass 78 percent and
nn
91 percent of the total spectrum energy, respectively. The Rayleigh bandwidth
β is used here to estimate appropriate range sampling rates, i.e., the sampling
r
rate F = β , so the sampling interval in fast time is T = 1/F = 1/β . The
s
s
r
r
s
corresponding range bin spacing is

(3.1)

In practice, the fast time signal is often sampled at some margin above the
Nyquist rate. This compensates both for the transition band of receiver
antialiasing filters and for some of the non-bandlimited nature of common pulse
waveforms. Sampling rate margins of 20 to 50 percent are common.

It will be seen in Chap. 4 that pulses are often phase modulated in order to
increase their bandwidth. The pulse spectrum is then no longer a sinc function.