Page 67 - Fundamentals of Radar Signal Processing

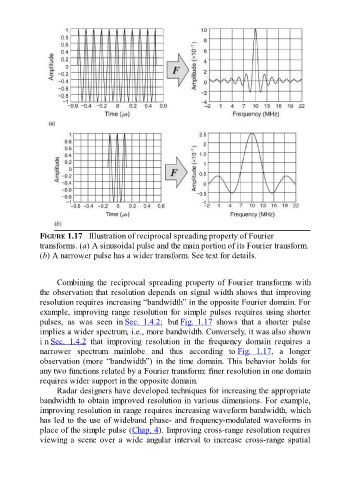
FIGURE 1.17 Illustration of reciprocal spreading property of Fourier
transforms. (a) A sinusoidal pulse and the main portion of its Fourier transform.
(b) A narrower pulse has a wider transform. See text for details.

Combining the reciprocal spreading property of Fourier transforms with
the observation that resolution depends on signal width shows that improving

resolution requires increasing “bandwidth” in the opposite Fourier domain. For
example, improving range resolution for simple pulses requires using shorter
pulses, as was seen in Sec. 1.4.2; but Fig. 1.17 shows that a shorter pulse
implies a wider spectrum, i.e., more bandwidth. Conversely, it was also shown
i n Sec. 1.4.2 that improving resolution in the frequency domain requires a
narrower spectrum mainlobe and thus according to Fig. 1.17, a longer
observation (more “bandwidth”) in the time domain. This behavior holds for

any two functions related by a Fourier transform: finer resolution in one domain
requires wider support in the opposite domain.
Radar designers have developed techniques for increasing the appropriate
bandwidth to obtain improved resolution in various dimensions. For example,
improving resolution in range requires increasing waveform bandwidth, which
has led to the use of wideband phase- and frequency-modulated waveforms in

place of the simple pulse (Chap. 4). Improving cross-range resolution requires
viewing a scene over a wide angular interval to increase cross-range spatial