Page 405 - Fundamentals of Reservoir Engineering

IMMISCIBLE DISPLACEMENT 340

Starting at point A, with the core sample 100% saturated with water, the water is
displaced by the oil, which is a drainage process. If the difference in phase pressures
(imposed pressure differential) is plotted as a function of the decreasing water
saturation the result would be the dashed line shown in fig. 10.3, the capillary pressure
drainage curve. At the connate water saturation (point B) there is an apparent
discontinuity at which the water saturation cannot be reduced further, irrespective of
the imposed difference in phase (capillary) pressure. If the experiment is reversed, by
displacing the oil with water, the result would be the imbibition curve shown as the solid
line in fig. 10.3. The drainage and imbibition plots differ due to the hysteresis in contact
angle, the latter being the one required for the displacement described in this chapter.
When the water saturation has risen to its maximum value S w = 1 − S or the capillary
pressure is zero (point C). At this point the residual oil saturation, S or, cannot be
reduced, irrespective of the pressure difference applied between the water and oil
(P c−negative).

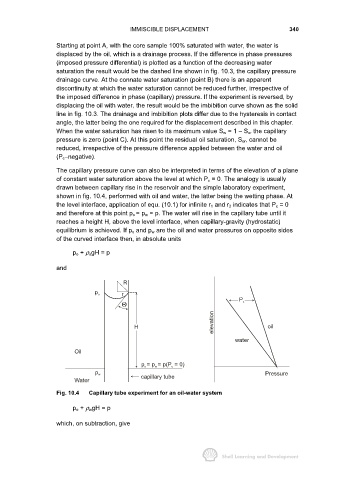
The capillary pressure curve can also be interpreted in terms of the elevation of a plane
of constant water saturation above the level at which P c = 0. The analogy is usually
drawn between capillary rise in the reservoir and the simple laboratory experiment,
shown in fig. 10.4, performed with oil and water, the latter being the wetting phase. At
the level interface, application of equ. (10.1) for infinite r 1 and r 2 indicates that P c = 0
and therefore at this point p o = p w = p. The water will rise in the capillary tube until it
reaches a height H, above the level interface, when capillary-gravity (hydrostatic)
equilibrium is achieved. If p o and p w are the oil and water pressures on opposite sides
of the curved interface then, in absolute units

p o + ρ ogH = p

and

R
p o r
P c
Θ
elevation

H oil

water
Oil

p= p = p(P = 0)
o w c
Pressure
p w capillary tube
Water
Fig. 10.4 Capillary tube experiment for an oil-water system

p o + ρ wgH = p

which, on subtraction, give