Page 175 - Fundamentals of The Finite Element Method for Heat and Fluid Flow

TRANSIENT HEAT CONDUCTION ANALYSIS
0.5 T = −45.0°C Insulated T l = −0.15°C 167
T s = −10.15°C
4

Figure 6.14 A one-dimensional solidification problem

side face is subjected to a liquidus temperature of −0.15 C. The solidus temperature is
◦
◦
−10.15 C. Determine the temperature distribution with respect to time if the latent heat of
solidification is 70.26, ρc p = 1.0 and k = 1.0. Draw the temperature variation at a distance
of unity from the left side with respect to time.
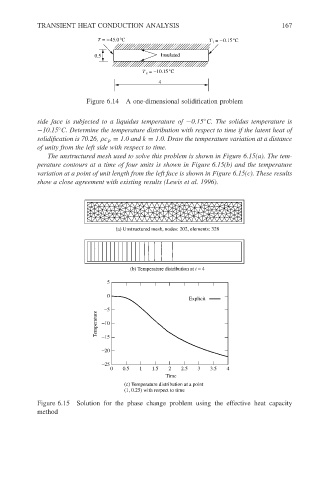
The unstructured mesh used to solve this problem is shown in Figure 6.15(a). The tem-
perature contours at a time of four units is shown in Figure 6.15(b) and the temperature
variation at a point of unit length from the left face is shown in Figure 6.15(c). These results
show a close agreement with existing results (Lewis et al. 1996).

(a) Unstructured mesh, nodes: 202, elements: 328

(b) Temperature distribution at t = 4
5

0
Explicit
−5
Temperature −10

−15

−20
−25
0 0.5 1 1.5 2 2.5 3 3.5 4
Time
(c) Temperature distribution at a point
(1, 0.25) with respect to time
Figure 6.15 Solution for the phase change problem using the effective heat capacity
method