Page 743 - Fundamentals of Water Treatment Unit Processes : Physical, Chemical, and Biological

698 Fundamentals of Water Treatment Unit Processes: Physical, Chemical, and Biological

0.8
BOX 22.4 KINETICS IN ACTIVATED SLUDGE
0.7
One of the first inklings that reaction stoichiometry and
0.6
Monod kinetics had entered activated-sludge reactor the-
ory was a paper by Garrett and Sawyer (1952, p. 51), 0.5
who referred to the relationship between cell growth and μ (h –1 ) 0.4
the removal of substrate and, in words (p. 75), described 0.3
a loading parameter, S o =Dt)=X, as kg substrate added per
0.2
day divided by the mass of viable cells under aeration,
0.1
which is the F=M ratio, i.e., F=M S o =uX (Tchobano-
glous and Burton, 1991, p. 389). They also described the 0.0
0 50 100 150 200 250 300
Monod equation but did not utilize it in analysis of their
data. The idea was extended by Eckenfelder and Weston (a) S (mg/L)
(1956, pp. 21–24), who showed a relation between net 400
cell production and substrate utilization, DX ¼ YDS,
350
Equation 22.19, a key part of a kinetic model.
In his doctoral thesis Andrew Gram III integrated the
complete-mix concept (pp. 11, 12) and the Monod kin- 250
etics equation (p. 20) into a reactor mass balance model S/μ (mg/L/h –1 ) 300
200
(Gram, 1956). Gram confirmed the validity of the 150
Monod equation (p. 122) for his model, but in describing
100
results, he deferred (p. 121) mostly to the ‘‘loading
50
velocity’’ (S o S)=(u X), which is defined currently as
the ‘‘substrate utilization rate,’’ U (Tchobanoglous and 0
0 50 100 150 200 250 300
Burton, 1991, p. 388), which is the same as m=Y.
Gram did not publish his work, but the Monod (b) S (mg/L)
equation was applied by Stewart et al. (1959) as related
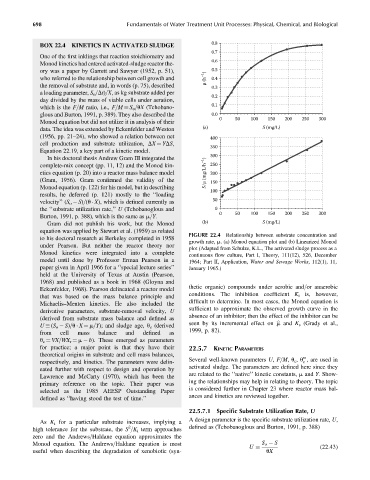
FIGURE 22.4 Relationship between substrate concentration and
to his doctoral research at Berkeley completed in 1958
growth rate, m. (a) Monod equation plot and (b) Linearized Monod
under Pearson. But neither the reactor theory nor
plot (Adapted from Schulze, K.L., The activated sludge process as a
Monod kinetics were integrated into a complete
continuous flow culture, Part I, Theory, 111(12), 526, December
model until done by Professor Erman Pearson in a 1964; Part II, Application, Water and Sewage Works, 112(1), 11,
paper given in April 1966 for a ‘‘special lecture series’’ January 1965.)
held at the University of Texas at Austin (Pearson,
1968) and published as a book in 1968 (Gloyna and
Eckenfelder, 1968). Pearson delineated a reactor model thetic organic) compounds under aerobic and=or anaerobic
that was based on the mass balance principle and conditions. The inhibition coefficient K i is, however,
difficult to determine. In most cases, the Monod equation is
Michaelis–Menten kinetics. He also included the
sufficient to approximate the observed growth curve in the
derivative parameters, substrate-removal velocity, U
absence of an inhibitor; then the effect of the inhibitor can be
(derived from substrate mass balance and defined as
seen by its incremental effect on bm and K s (Grady et al.,
U (S o S)=u X ¼ m=Y); and sludge age, u c (derived
1999, p. 82).
from cell mass balance and defined as
u c ¼ VX=WX r ¼ m b). These emerged as parameters
for practice; a major point is that they have their 22.5.7 KINETIC PARAMETERS
theoretical origins in substrate and cell mass balances, m
Several well-known parameters U, F=M, u c , u , are used in
respectively, and kinetics. The parameters were delin- c
activated sludge. The parameters are defined here since they
eated further with respect to design and operation by
are related to the ‘‘native’’ kinetic constants, m and Y. Show-
Lawrence and McCarty (1970), which has been the
ing the relationships may help in relating to theory. The topic
primary reference on the topic. Their paper was
is considered further in Chapter 23 where reactor mass bal-
selected as the 1985 AEESP Outstanding Paper
defined as ‘‘having stood the test of time.’’ ances and kinetics are reviewed together.
22.5.7.1 Specific Substrate Utilization Rate, U
A design parameter is the specific substrate utilization rate, U,
As K i for a particular substrate increases, implying a
2 defined as (Tchobanoglous and Burton, 1991, p. 388)
high tolerance for the substrate, the S =K i term approaches
zero and the Andrews=Haldane equation approximates the
Monod equation. The Andrews=Haldane equation is most S o S
(22:43)
U
useful when describing the degradation of xenobiotic (syn- uX