Page 219 - gas transport in porous media

Chapter 12: Continuum Modeling of Gas Transport in Porous Media
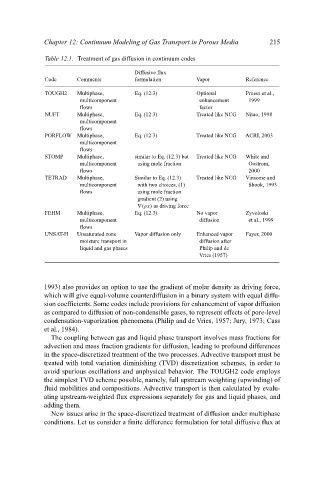
Table 12.1. Treatment of gas diffusion in continuum codes
Diffusive flux 215
Code Comments formulation Vapor Reference
TOUGH2 Multiphase, Eq. (12.3) Optional Pruess et al.,
multicomponent enhancement 1999
flows factor
NUFT Multiphase, Eq. (12.3) Treated like NCG Nitao, 1998
multicomponent
flows
PORFLOW Multiphase, Eq. (12.3) Treated like NCG ACRI, 2003
multicomponent
flows
STOMP Multiphase, similar to Eq. (12.3) but Treated like NCG White and
multicomponent using mole fraction Oostrom,
flows 2000
TETRAD Multiphase, Similar to Eq. (12.3) Treated like NCG Vinsome and
multicomponent with two choices, (1) Shook, 1993
flows using mole fraction
gradient (2) using
∇(ρx) as driving force
FEHM Multiphase, Eq. (12.3) No vapor Zyvoloski
multicomponent diffusion et al., 1999
flows
UNSAT-H Unsaturated zone Vapor diffusion only Enhanced vapor Fayer, 2000
moisture transport in diffusion after
liquid and gas phases Philip and de
Vries (1957)

1993) also provides an option to use the gradient of molar density as driving force,
which will give equal-volume counterdiffusion in a binary system with equal diffu-
sion coefficients. Some codes include provisions for enhancement of vapor diffusion
as compared to diffusion of non-condensible gases, to represent effects of pore-level
condensation-vaporization phenomena (Philip and de Vries, 1957; Jury, 1973; Cass
et al., 1984).
The coupling between gas and liquid phase transport involves mass fractions for
advection and mass fraction gradients for diffusion, leading to profound differences
in the space-discretized treatment of the two processes. Advective transport must be
treated with total variation diminishing (TVD) discretization schemes, in order to
avoid spurious oscillations and unphysical behavior. The TOUGH2 code employs
the simplest TVD scheme possible, namely, full upstream weighting (upwinding) of
fluid mobilities and compositions. Advective transport is then calculated by evalu-
ating upstream-weighted flux expressions separately for gas and liquid phases, and
adding them.
New issues arise in the space-discretized treatment of diffusion under multiphase
conditions. Let us consider a finite difference formulation for total diffusive flux at