Page 39 - gas transport in porous media

Ho
32
σ is the surface tension of the liquid [N/m], r 1 and r 2 are the radii of curvature
[m] of the liquid–vapor interface. Equation (3.9) is derived by equating the chemical
potential of the liquid and vapor phases, and Equation (3.10) is derived through either
force-balance relations or thermodynamic analysis of the interfacial region (Carey,
1992). It should be noted that the “complete” Kelvin equation includes an additional
term inside the exponential in Equation (3.9) that is negligible in most situations
except in high-pressure systems (Elliott, 2001). In addition, for capillary tubes, the
radii of curvature of the meniscus are equal and related to the radius of the capillary
tube, r, and the contact angle, θ, by the following expression:

r 1 = r 2 = r/ cos(θ) (3.11)

As the radii of curvature are reduced (i.e., smaller pores), the capillary pressure
is increased and the resulting partial pressure in the gas phase is decreased. Note
that Equation (3.9) can also be expressed as the ratio of the partial vapor pressure
to the saturated vapor pressure (P v /P sat ). For water, this ratio expresses the relative
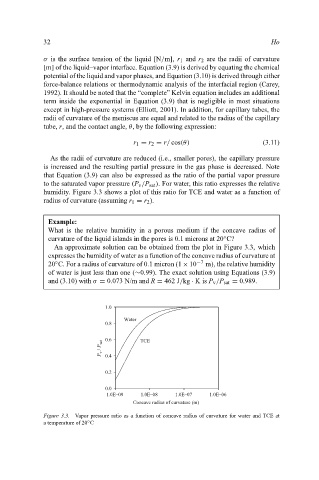
humidity. Figure 3.3 shows a plot of this ratio for TCE and water as a function of
radius of curvature (assuming r 1 = r 2 ).

Example:
What is the relative humidity in a porous medium if the concave radius of
◦
curvature of the liquid islands in the pores is 0.1 microns at 20 C?
An approximate solution can be obtained from the plot in Figure 3.3, which
expresses the humidity of water as a function of the concave radius of curvature at
◦
20 C. For a radius of curvature of 0.1 micron (1 × 10 −7 m), the relative humidity
of water is just less than one (∼0.99). The exact solution using Equations (3.9)
and (3.10) with σ = 0.073 N/m and R = 462 J/kg · Kis P v /P sat = 0.989.

1.0

Water
0.8
P v / P sat 0.6 TCE

0.4

0.2

0.0
1.0E–09 1.0E–08 1.0E–07 1.0E–06
Concave radius of curvature (m)
Figure 3.3. Vapor pressure ratio as a function of concave radius of curvature for water and TCE at
a temperature of 20 C
◦