Page 21 - Geochemical Anomaly and Mineral Prospectivity Mapping in GIS

16 Chapter 1

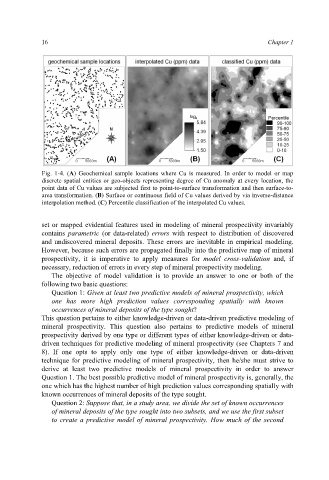
Fig. 1-4. (A) Geochemical sample locations where Cu is measured. In order to model or map
discrete spatial entities or geo-objects representing degree of Cu anomaly at every location, the
point data of Cu values are subjected first to point-to-surface transformation and then surface-to-
area transformation. (B) Surface or continuous field of Cu values derived by via inverse-distance
interpolation method. (C) Percentile classification of the interpolated Cu values.

set or mapped evidential features used in modeling of mineral prospectivity invariably
contains parametric (or data-related) errors with respect to distribution of discovered
and undiscovered mineral deposits. These errors are inevitable in empirical modeling.
However, because such errors are propagated finally into the predictive map of mineral
prospectivity, it is imperative to apply measures for model cross-validation and, if
necessary, reduction of errors in every step of mineral prospectivity modeling.
The objective of model validation is to provide an answer to one or both of the
following two basic questions:
Question 1: Given at least two predictive models of mineral prospectivity, which
one has more high prediction values corresponding spatially with known
occurrences of mineral deposits of the type sought?
This question pertains to either knowledge-driven or data-driven predictive modeling of
mineral prospectivity. This question also pertains to predictive models of mineral
prospectivity derived by one type or different types of either knowledge-driven or data-
driven techniques for predictive modeling of mineral prospectivity (see Chapters 7 and
8). If one opts to apply only one type of either knowledge-driven or data-driven
technique for predictive modeling of mineral prospectivity, then he/she must strive to
derive at least two predictive models of mineral prospectivity in order to answer
Question 1. The best possible predictive model of mineral prospectivity is, generally, the
one which has the highest number of high prediction values corresponding spatially with
known occurrences of mineral deposits of the type sought.
Question 2: Suppose that, in a study area, we divide the set of known occurrences
of mineral deposits of the type sought into two subsets, and we use the first subset
to create a predictive model of mineral prospectivity. How much of the second