Page 208 - Geology of Carbonate Reservoirs

FRACTURE PERMEABILITY, POROSITY, AND S W 189

60 acres
40 acres 160 acres
2.5
Fracture Porosity % 1.5 320 acres
2.0

1.0
640 acres
0.5
0
0 200 400 600 400 1000 1200 1400 1600 1800 2000 2200 2400 2600 2800 3000
Fracture Volume in Thousands of Reservoir Barrels

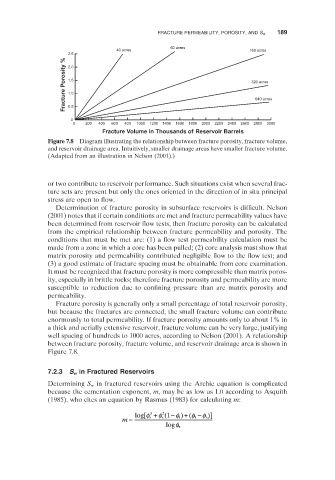
Figure 7.8 Diagram illustrating the relationship between fracture porosity, fracture volume,

and reservoir drainage area. Intuitively, smaller drainage areas have smaller fracture volume.
(Adapted from an illustration in Nelson (2001) .)

or two contribute to reservoir performance. Such situations exist when several frac-
ture sets are present but only the ones oriented in the direction of in situ principal
stress are open to fl ow.
Determination of fracture porosity in subsurface reservoirs is diffi cult. Nelson
(2001) notes that if certain conditions are met and fracture permeability values have
been determined from reservoir flow tests, then fracture porosity can be calculated

from the empirical relationship between fracture permeability and porosity. The
conditions that must be met are: (1) a flow test permeability calculation must be

made from a zone in which a core has been pulled; (2) core analysis must show that
matrix porosity and permeability contributed negligible flow to the flow test; and

(3) a good estimate of fracture spacing must be obtainable from core examination.
It must be recognized that fracture porosity is more compressible than matrix poros-
ity, especially in brittle rocks; therefore fracture porosity and permeability are more
susceptible to reduction due to confining pressure than are matrix porosity and

permeability.
Fracture porosity is generally only a small percentage of total reservoir porosity,
but because the fractures are connected, the small fracture volume can contribute
enormously to total permeability. If fracture porosity amounts only to about 1% in
a thick and aerially extensive reservoir, fracture volume can be very large, justifying
well spacing of hundreds to 1000 acres, according to Nelson (2001) . A relationship
between fracture porosity, fracture volume, and reservoir drainage area is shown in
Figure 7.8 .

7.2.3 S w in Fractured Reservoirs

Determining S w in fractured reservoirs using the Archie equation is complicated
because the cementation exponent, m , may be as low as 1.0 according to Asquith
(1985) , who cites an equation by Rasmus (1983) for calculating m :
3 2 (1 + − )]
m = log[φ s + φ s − ) (φ t φ s
φ t
logφ t