Page 284 - Global Tectonics

SUBDUCTION ZONES 269

(a) 3

4 Accreted sediment Décollement
0.40
Depth (km) 5 0.60
6
7 0.80 Underthrust sediment Surface slope
8 Taper angle Subduction angle

50 40 30 20 10 0
Distance arcward from the deformation front (km)
(b)
Well drained: Poorly drained:
Rapid fluid escape Retarded fluid escape
Low pore pressures Elevated pore
pressures

Wedge steepens Wedge remains
TIME shallow

Steep stable geometry Shallow stable geometry
Strong base Weak base

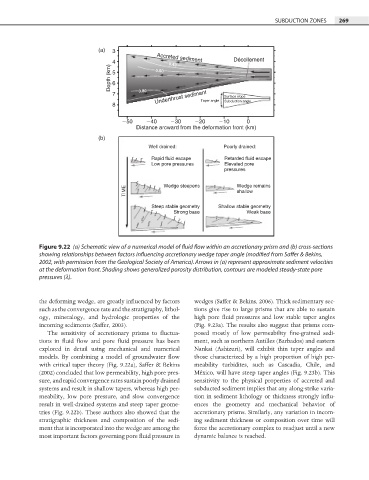
Figure 9.22 (a) Schematic view of a numerical model of fluid flow within an accretionary prism and (b) cross-sections

showing relationships between factors influencing accretionary wedge taper angle (modified from Saffer & Bekins,

2002, with permission from the Geological Society of America). Arrows in (a) represent approximate sediment velocities
at the deformation front. Shading shows generalized porosity distribution, contours are modeled steady-state pore
pressures (l).

the deforming wedge, are greatly influenced by factors wedges (Saffer & Bekins, 2006). Thick sedimentary sec-
such as the convergence rate and the stratigraphy, lithol- tions give rise to large prisms that are able to sustain

ogy, mineralogy, and hydrologic properties of the high pore fluid pressures and low stable taper angles
incoming sediments (Saffer, 2003). (Fig. 9.23a). The results also suggest that prisms com-
The sensitivity of accretionary prisms to fl uctua- posed mostly of low permeability fi ne-grained sedi-
tions in fl uid flow and pore fluid pressure has been ment, such as northern Antilles (Barbados) and eastern

explored in detail using mechanical and numerical Nankai (Ashizuri), will exhibit thin taper angles and
models. By combining a model of groundwater fl ow those characterized by a high proportion of high per-
with critical taper theory (Fig. 9.22a), Saffer & Bekins meability turbidites, such as Cascadia, Chile, and
(2002) concluded that low permeability, high pore pres- México, will have steep taper angles (Fig. 9.23b). This
sure, and rapid convergence rates sustain poorly drained sensitivity to the physical properties of accreted and
systems and result in shallow tapers, whereas high per- subducted sediment implies that any along-strike varia-
meability, low pore pressure, and slow convergence tion in sediment lithology or thickness strongly infl u-
result in well-drained systems and steep taper geome- ences the geometry and mechanical behavior of
tries (Fig. 9.22b). These authors also showed that the accretionary prisms. Similarly, any variation in incom-
stratigraphic thickness and composition of the sedi- ing sediment thickness or composition over time will
ment that is incorporated into the wedge are among the force the accretionary complex to readjust until a new

most important factors governing pore fluid pressure in dynamic balance is reached.