Page 292 - Geology and Geochemistry of Oil and Gas

254 MATHEMATICAL MODELING IN PETROLEUM GEOLOGY

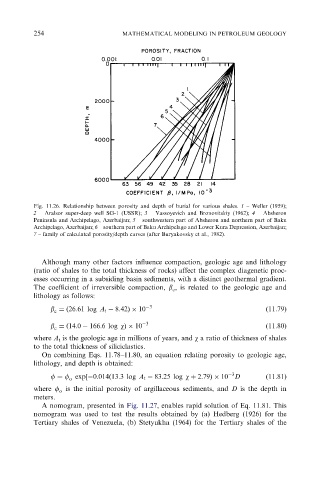
Fig. 11.26. Relationship between porosity and depth of burial for various shales. 1 – Weller (1959);
2 – Aralsor super-deep well SG-1 (USSR); 3 – Vassoyevich and Bronovitskiy (1962); 4 – Absheron
Peninsula and Archipelago, Azerbaijan; 5 – southwestern part of Absheron and northern part of Baku
Archipelago, Azerbaijan; 6 – southern part of Baku Archipelago and Lower Kura Depression, Azerbaijan;
7 – family of calculated porosity/depth curves (after Buryakovsky et al., 1982).

Although many other factors influence compaction, geologic age and lithology
(ratio of shales to the total thickness of rocks) affect the complex diagenetic proc-
esses occurring in a subsiding basin sediments, with a distinct geothermal gradient.
The coefficient of irreversible compaction, b , is related to the geologic age and
c
lithology as follows:
b ¼ ð26:61 log A t 8:42Þ 10 3 (11.79)
c
b ¼ ð14:0 166:6 log wÞ 10 3 (11.80)
c
where A t is the geologic age in millions of years, and w a ratio of thickness of shales
to the total thickness of siliciclastics.
On combining Eqs. 11.78–11.80, an equation relating porosity to geologic age,
lithology, and depth is obtained:
3
f ¼ f exp½ 0:014ð13:3 log A t 83:25 log w þ 2:79Þ 10 D (11.81)
o
where f is the initial porosity of argillaceous sediments, and D is the depth in
o
meters.
A nomogram, presented in Fig. 11.27, enables rapid solution of Eq. 11.81. This
nomogram was used to test the results obtained by (a) Hedberg (1926) for the
Tertiary shales of Venezuela, (b) Stetyukha (1964) for the Tertiary shales of the