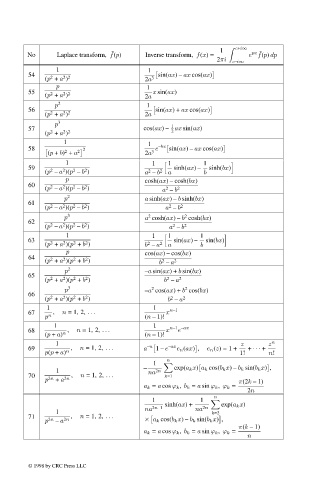
Page 740 - Handbook Of Integral Equations

1 c+i∞ px ˜
˜
No Laplace transform, f(p) Inverse transform, f(x)= e f(p) dp
2πi
c–i∞
1 1
54 2 2 2 sin(ax) – ax cos(ax)
(p + a ) 2a 3
p 1
55 2 2 2 x sin(ax)
(p + a ) 2a
p 2 1
56 sin(ax)+ ax cos(ax)
2 2
2
(p + a ) 2a
p 3 1
57 cos(ax) – ax sin(ax)
2
2 2
2
(p + a )
1 1
58 2 e –bx sin(ax) – ax cos(ax)
(p + b) + a 2 2a 3
2
1 1 1 1
59 sinh(ax) – sinh(bx)
2
(p – a )(p – b ) a – b 2 a b
2
2
2
2
p cosh(ax) – cosh(bx)
60 2 2 2 2
(p – a )(p – b ) a – b 2
2
p 2 a sinh(ax) – b sinh(bx)
61
2
2
2
2
2
(p – a )(p – b ) a – b 2
2
2
p 3 a cosh(ax) – b cosh(bx)
62 2 2 2 2
2
(p – a )(p – b ) a – b 2
1 1 1 1
63 sin(ax) – sin(bx)
2
2
2
2
(p + a )(p + b ) b – a 2 a b
2
p cos(ax) – cos(bx)
64 2 2 2 2
(p + a )(p + b ) b – a 2
2
p 2 –a sin(ax)+ b sin(bx)
65
2
2
2
2
2
(p + a )(p + b ) b – a 2
2
2
p 3 –a cos(ax)+ b cos(bx)
66 2 2 2 2
(p + a )(p + b ) b – a 2
2
1 1 n–1
67 , n =1, 2, ... x
p n (n – 1)!
1 1 n–1 –ax
68 n , n =1, 2, ... x e
(p + a) (n – 1)!
1 z z n
69 n , n =1, 2, ... a –n 1 – e –ax e n (ax) , e n (z)=1 + + ··· +
p(p + a) 1! n!
n
1
– exp(a k x) a k cos(b k x) – b k sin(b k x) ,
1 na 2n
70 2n 2n , n =1, 2, ... k=1
p + a π(2k – 1)
a k = a cos ϕ k , b k = a sin ϕ k , ϕ k =
2n
n
1 1
sinh(ax)+ exp(a k x)
na 2n–1 na 2n
1 k=2
71 , n =1, 2, ...
p 2n – a 2n × a k cos(b k x) – b k sin(b k x) ,
π(k – 1)
a k = a cos ϕ k , b k = a sin ϕ k , ϕ k =
n
© 1998 by CRC Press LLC
© 1998 by CRC Press LLC
Page 724