Page 470 - High Power Laser Handbook

438 Fi b er L a s er s Intr oduction to Optical Fiber Lasers 439

It was shown early on that the composite cladding’s effective
refractive index can be represented by the effective mode index of the
fundamental mode of an infinite medium, which consists of the clad-
30
ding’s basic unit cell extending to infinity in all directions. This
mode is referred to as fundamental space-filling mode with effective
index n FSM , which can be obtained through a mode solver. It took a
few years until it was determined that the core radius is better approx-
, where Λ is the center-to-center spacing of the
imated by Λ/3 1/2 36
holes and d is usually used to represent the hole diameter. The unique
scaling properties of the Helmholtz eigenvalue equation dictate that
the modes of a waveguide are not fundamentally changed in terms of
modal properties when all length-related properties (x, y, and λ) are
scaled by the same amount. This property is useful because it means
that such waveguides can be analyzed efficiently using normalized
parameters. It is common to plot the solutions in normalized length
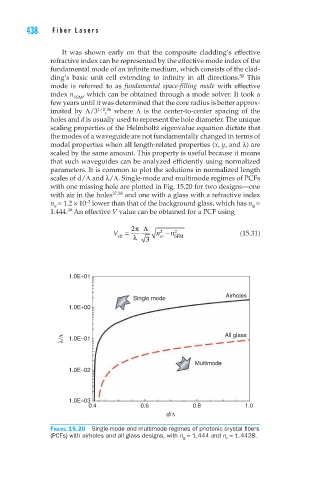
scales of d/Λ and λ/Λ. Single-mode and multimode regimes of PCFs
with one missing hole are plotted in Fig. 15.20 for two designs—one
with air in the holes 37,38 and one with a glass with a refractive index
–3
n = 1.2 × 10 lower than that of the background glass, which has n =
F
B
39
1.444. An effective V value can be obtained for a PCF using
2π Λ
V = eff n − co 2 n 2 SFM (15.31)
λ 3

1.0E+01

Airholes
Single mode
1.0E+00

λ/Λ 1.0E−01 All glass

Multimode
1.0E−02

1.0E−03
0.4 0.6 0.8 1.0
d/Λ
Figure 15.20 Single-mode and multimode regimes of photonic crystal fibers
(PCFs) with airholes and all glass designs, with n = 1.444 and n = 1.4428.
B F