Page 98 - High Power Laser Handbook

68 G a s , C h e m i c a l , a n d F r e e - E l e c t r o n L a s e r s Chemical Lasers 69

20
v ≈ 24

I (B)
2
15 O 2 ( Σ)
1
Energy (cm −1 × 10 −3 ) 10 v = 2 I + I
I (A)

2
I (A′)
v = 1
2

1
I*
2
−1
∆E = 279 cm O ( ∆) 500–700 nm
5 762 nm 1.0–1.5 µm
1.315 µm
1.27 µm
3
0 I O ( Σ) I 2 (X)
2
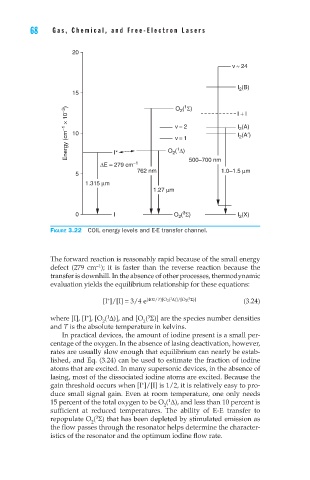
Figure 3.22 COIL energy levels and E-E transfer channel.

The forward reaction is reasonably rapid because of the small energy
–1
defect (279 cm ); it is faster than the reverse reaction because the
transfer is downhill. In the absence of other processes, thermodynamic
evaluation yields the equilibrium relationship for these equations:
3
*
1
[I ]/[I] = 3/4 e (402/T)[O 2( ∆)]/[O 2( Σ)] (3.24)
3
1
where [I], [I ], [O ( ∆)], and [O ( Σ)] are the species number densities
*
2
2
and T is the absolute temperature in kelvins.
In practical devices, the amount of iodine present is a small per-
centage of the oxygen. In the absence of lasing deactivation, however,
rates are usually slow enough that equilibrium can nearly be estab-
lished, and Eq. (3.24) can be used to estimate the fraction of iodine
atoms that are excited. In many supersonic devices, in the absence of
lasing, most of the dissociated iodine atoms are excited. Because the
*
gain threshold occurs when [I ]/[I] is 1/2, it is relatively easy to pro-
duce small signal gain. Even at room temperature, one only needs
1
15 percent of the total oxygen to be O ( ∆), and less than 10 percent is
2
sufficient at reduced temperatures. The ability of E-E transfer to
repopulate O ( Σ) that has been depleted by stimulated emission as
3
2
the flow passes through the resonator helps determine the character-
istics of the resonator and the optimum iodine flow rate.