Page 164 - How To Solve Word Problems In Calculus

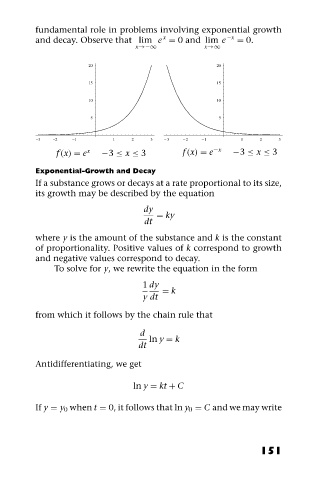
fundamental role in problems involving exponential growth
x
and decay. Observe that lim e = 0 and lim e −x = 0.
x→−∞ x→∞
20 20

15 15

10 10
5 5

−3 −2 −1 1 2 3 −3 −2 −1 1 2 3
f (x) = e x −3 ≤ x ≤ 3 f (x) = e −x −3 ≤ x ≤ 3

Exponential-Growth and Decay
If a substance grows or decays at a rate proportional to its size,
its growth may be described by the equation
dy
= ky
dt
where y is the amount of the substance and k is the constant
of proportionality. Positive values of k correspond to growth
and negative values correspond to decay.
To solve for y, we rewrite the equation in the form
1 dy
= k
y dt

from which it follows by the chain rule that

d
ln y = k
dt

Antidifferentiating, we get

ln y = kt + C

If y = y 0 when t = 0, it follows that ln y 0 = C and we may write

151