Page 44 - Hydrogeology Principles and Practice

HYDC02 12/5/05 5:37 PM Page 27

Physical hydrogeology 27

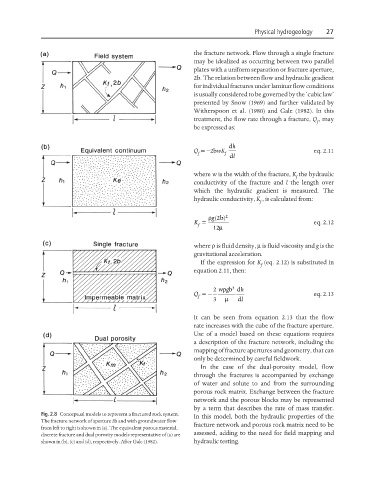
the fracture network. Flow through a single fracture
may be idealized as occurring between two parallel
plates with a uniform separation or fracture aperture,
2b. The relation between flow and hydraulic gradient
for individual fractures under laminar flow conditions
is usually considered to be governed by the ‘cubic law’
presented by Snow (1969) and further validated by
Witherspoon et al. (1980) and Gale (1982). In this
treatment, the flow rate through a fracture, Q , may
f
be expressed as:

dh
Q =−2bwK eq. 2.11
f f
dl
where w is the width of the fracture, K the hydraulic
f
conductivity of the fracture and l the length over
which the hydraulic gradient is measured. The
hydraulic conductivity, K , is calculated from:
f
ρ 2b 2
g()
K = eq. 2.12
f µ
12
where ρ is fluid density, µ is fluid viscosity and g is the
gravitational acceleration.
If the expression for K (eq. 2.12) is substituted in
f
equation 2.11, then:

3
Q =− 2 wg ρ bd h eq. 2.13

f µ
3 l d
It can be seen from equation 2.13 that the flow
rate increases with the cube of the fracture aperture.
Use of a model based on these equations requires
a description of the fracture network, including the
mapping of fracture apertures and geometry, that can
only be determined by careful fieldwork.
In the case of the dual-porosity model, flow
through the fractures is accompanied by exchange
of water and solute to and from the surrounding
porous rock matrix. Exchange between the fracture
network and the porous blocks may be represented
by a term that describes the rate of mass transfer.
Fig. 2.8 Conceptual models to represent a fractured rock system.
In this model, both the hydraulic properties of the
The fracture network of aperture 2b and with groundwater flow
fracture network and porous rock matrix need to be
from left to right is shown in (a). The equivalent porous material,
assessed, adding to the need for field mapping and
discrete fracture and dual porosity models representative of (a) are
shown in (b), (c) and (d), respectively. After Gale (1982). hydraulic testing.