Page 45 - Hydrogeology Principles and Practice

HYDC02 12/5/05 5:37 PM Page 28

28 Chapter Two

BO X
Laminar and turbulent flows
2.2

Darcy’s law applies when flow is laminar but at high flow velocities,
turbulent flow occurs and Darcy’s law breaks down. Under laminar
conditions individual ‘particles’ of water move in paths parallel to
the direction of flow, with no mixing or transverse component to the
fluid motion. These conditions can be visualized by making an analogy
between flow in a straight, cylindrical tube of constant diameter,
and flow through porous granular or fissured material. At the edge
of the tube, the flow velocity is zero rising to a maximum at the cen-
tre. As the flow velocity increases, so fluctuating eddies develop and
transverse mixing occurs whereupon the flow becomes turbulent.
Flow rates that exceed the upper limit of Darcy’s law are common
in karstic limestones (Section 2.7) and dolomites and highly perme-
able volcanic formations. Also, the high velocities experienced close
to the well screen of a pumping borehole can create turbulent
conditions. The change from laminar flow at low velocities to turbul-
ent flow at high velocities is usually related to the dimensionless
Reynolds number, R , which expresses the ratio of inertial to viscous
e
forces during flow. For flow through porous material, the Reynolds
number is expressed as follows:

r qd
R = eq. 1
e m

where r is fluid density, m is viscosity and q is the specific discharge
(or characteristic velocity for fissured or fractured material). The char-
acteristic length, d, can represent the mean pore diameter, mean
grain diameter or, in the case of a fissure or fracture, either the hydraulic
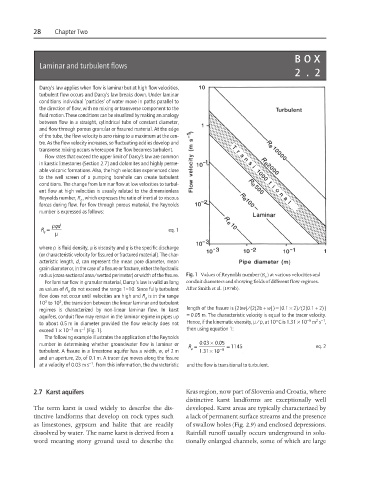
radius (cross-sectional area/wetted perimeter) or width of the fissure. Fig. 1 Values of Reynolds number (R ) at various velocities and
e
For laminar flow in granular material, Darcy’s law is valid as long conduit diameters and showing fields of different flow regimes.
as values of R do not exceed the range 1–10. Since fully turbulent After Smith et al. (1976b).
e
flow does not occur until velocities are high and R is in the range
e
2
3
10 to 10 , the transition between the linear laminar and turbulent
regimes is characterized by non-linear laminar flow. In karst length of the fissure is (2bw)/(2(2b + w)) = (0.1 × 2)/(2(0.1 + 2) )
aquifers, conduit flow may remain in the laminar regime in pipes up = 0.05 m. The characteristic velocity is equal to the tracer velocity.
2 −1
−6
to about 0.5 m in diameter provided the flow velocity does not Hence, if the kinematic viscosity, m/r, at 10°C is 1.31 × 10 m s ,
−1
exceed 1 × 10 −3 ms (Fig. 1). then using equation 1:
The following example illustrates the application of the Reynolds
. 0
number in determining whether groundwater flow is laminar or R = 003 × .05 = 1145 eq. 2
turbulent. A fissure in a limestone aquifer has a width, w, of 2 m e 131 × −6
. 10
and an aperture, 2b, of 0.1 m. A tracer dye moves along the fissure
−1
at a velocity of 0.03 m s . From this information, the characteristic and the flow is transitional to turbulent.
2.7 Karst aquifers Kras region, now part of Slovenia and Croatia, where
distinctive karst landforms are exceptionally well
The term karst is used widely to describe the dis- developed. Karst areas are typically characterized by
tinctive landforms that develop on rock types such a lack of permanent surface streams and the presence
as limestones, gypsum and halite that are readily of swallow holes (Fig. 2.9) and enclosed depressions.
dissolved by water. The name karst is derived from a Rainfall runoff usually occurs underground in solu-
word meaning stony ground used to describe the tionally enlarged channels, some of which are large