Page 330 - Instant notes

Physical Chemistry 316

Rotational energy levels

Application of quantum theory shows that the rotational energy possessed by a
molecule is quantized, in the same way that all energy is quantized. In general, the rate
of rotation of a molecule is sufficiently slow compared with the rate of vibration of the
bonds, that the molecule can be considered as a rigid body rotating with fixed
internuclear separations given by the average of the vibrational displacements.

Diatomic molecule
The simplest type of rigid rotor is the linear rotor of a diatomic molecule. When the
Schrödinger equation is solved for a linear rigid rotor (see particle in a circular orbit,
Topic G4), the allowed energy levels turn out to be quantized according to:
E J=BJ(J+1) J=0, 1, 2,…

where J is the rotational quantum number, and

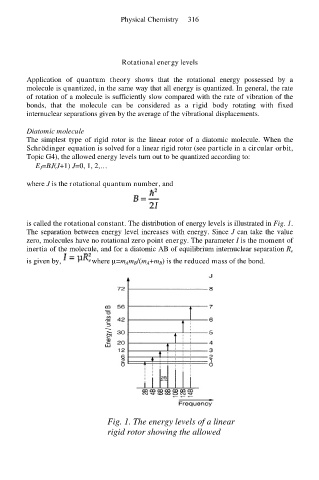
is called the rotational constant. The distribution of energy levels is illustrated in Fig. 1.
The separation between energy level increases with energy. Since J can take the value
zero, molecules have no rotational zero point energy. The parameter I is the moment of
inertia of the molecule, and for a diatomic AB of equilibrium internuclear separation R e
is given by, where µ=m Am B/(m A+m B) is the reduced mass of the bond.

Fig. 1. The energy levels of a linear
rigid rotor showing the allowed