Page 159 - Intelligent Digital Oil And Gas Fields

122 Intelligent Digital Oil and Gas Fields

4.2.2.1 Artificial Neural Network
ANNs are ML systems based on the workings of the brain, which is known
to consist of a massively interconnected system of neurons that do sensory
processing, control motor functions, and engage in patterns of thought.
ANNs are “trained” by a large number of input patterns that cause them
to “learn” from the experience from the bottom-up approach. The structure
of a neural network is usually drawn as a hierarchy of layers (input, hidden,
and output) in which nodes (representing neurons) are connected by arcs
(see Fig. 4.8A). The arithmetic value of any node is equal to the sum of
the values of the preceding nodes each multiplied by the weight of the con-
necting arc, called the activation function:

(4.1)
y i ¼ Σw ij x j
where y i is the value of the ith node, x i the value of the jth node of the
preceding layer, and w ij is the weight associated with the arch that connects
the two nodes. The output node is governed by the activation function
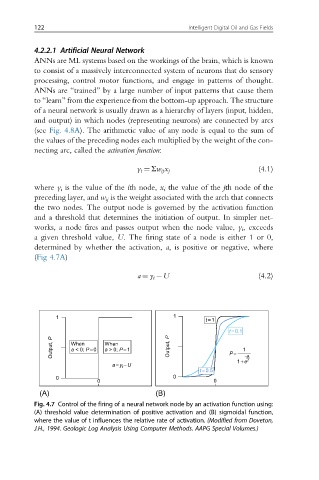
and a threshold that determines the initiation of output. In simpler net-
works, a node fires and passes output when the node value, y i , exceeds
a given threshold value, U. The firing state of a node is either 1 or 0,
determined by whether the activation, a, is positive or negative, where
(Fig 4.7A)

a ¼ y i U (4.2)

1 1
t=1
t=0.1
Output, P When When Output, P P= 1 −a
a > 0; P= 1
a < 0; P=0
a = y t − U 1+ e t
t =0.5
0 0
0 0
(A) (B)
Fig. 4.7 Control of the firing of a neural network node by an activation function using:
(A) threshold value determination of positive activation and (B) sigmoidal function,
where the value of t influences the relative rate of activation. (Modified from Doveton,
J.H., 1994. Geologic Log Analysis Using Computer Methods. AAPG Special Volumes.)