Page 52 - Introduction to Naval Architecture

FLOTATION AND STABILITY 39

The height of the metacentre depends upon the draught and beam but
not the length. At small draught relative to beam, the second term
predominates and at zero draught KM would be infinite.
To put some figures to this consider the case where B is 15m for
draughts varying from 1 to 6m. Then:

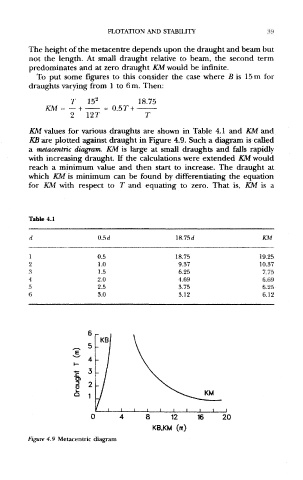
KM values for various draughts are shown in Table 4,1 and KM and
KB are plotted against draught in Figure 4.9. Such a diagram is called
a metacentric diagram. KM is large at small draughts and falls rapidly
with increasing draught. If the calculations were extended KM would
reach a minimum value and then start to increase. The draught at
which KM is minimum can be found by differentiating the equation
for KM with respect to T and equating to zero. That is, KM is a

Table 4.1

d 0.5 d 18.75d KM

I 0.5 18.75 19.25
2 1.0 9.37 10.37
3 1.5 6.25 7.75
4 2.0 4.69 6.69
5 2.5 3.75 6.25
6 3.0 3.12 6.12

Figure 4.9 Metacentric diagram