Page 204 - Introduction to Petroleum Engineering

PERFORATING 191

1.0

0.8
Productivity efficiency N pe 0.6

0.4

0.2

0.0
0.1 1 10 100 1000
N pd

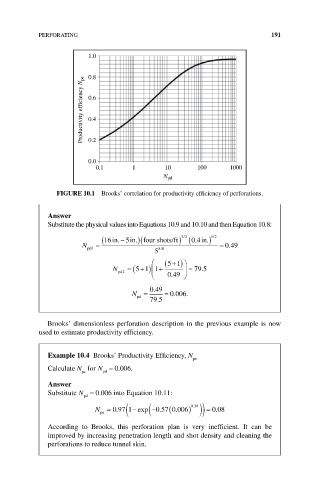
FIGURE 10.1 Brooks’ correlation for productivity efficiency of perforations.

Answer
Substitute the physical values into Equations 10.9 and 10.10 and then Equation 10.8:
16 ( in. 5 )( four shots/ft) ( 0 4 in ) . 12
/
/
32
−
.
in.
049
N = = .
pd1
/
5 58

+
=
N pd2 ( 51 1+ ( 51)   = 79 5.
+ )


.
 049 
049
.
N = = 0 006.
.
pd
79 5
.
Brooks’ dimensionless perforation description in the previous example is now
used to estimate productivity efficiency.
Example 10.4 Brooks’ Productivity Efficiency, N
pe
Calculate N for N = 0 006.
.
pe pd
Answer
Substitute N = 0 006 into Equation 10.11:
.
pd
(
(
038
.
−
N = 0971 exp ( −0570 006 ) )) = 008
.
.
.
.
pe
According to Brooks, this perforation plan is very inefficient. It can be
improved by increasing penetration length and shot density and cleaning the
perforations to reduce tunnel skin.