Page 146 - Introduction to chemical reaction engineering and kinetics

128 Chapter 6: Fundamentals of Reaction Rates

0 5 1 0 15 20 25
Ul
10-3EIJ mol-’ u/m I1
(a) (b)
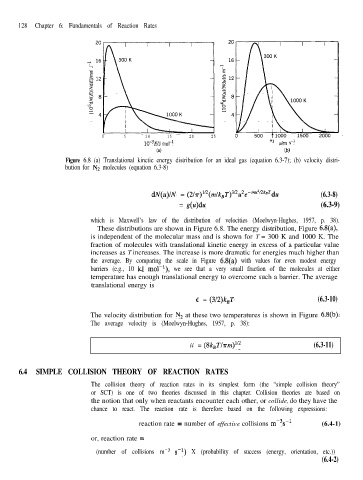
Figure 6.8 (a) Translational kinetic energy distribution for an ideal gas (equation 6.3-7); (b) velocity distri-
bution for N2 molecules (equation 6.3-8)

dN(u)lN = (2/~)1’2(mlkBT)3’2u2e-mu2’2kBTdu (6.3-8)
= g(u)du (6.3-9)

which is Maxwell’s law of the distribution of velocities (Moelwyn-Hughes, 1957, p. 38).
These distributions are shown in Figure 6.8. The energy distribution, Figure 6.8(a),
is independent of the molecular mass and is shown for T = 300 K and 1000 K. The
fraction of molecules with translational kinetic energy in excess of a particular value
increases as T increases. The increase is more dramatic for energies much higher than
the average. By comparing the scale in Figure 6.8(a) with values for even modest energy
barriers (e.g., 10 kJ mol-l), we see that a very small fraction of the molecules at either
temperature has enough translational energy to overcome such a barrier. The average
translational energy is
C = (3/2)k,T (6.3-10)

The velocity distribution for N2 at these two temperatures is shown in Figure 6.8(b).
The average velocity is (Moelwyn-Hughes, 1957, p. 38):

ii = (8kBThn)1’2 (6.3-11)

6.4 SIMPLE COLLISION THEORY OF REACTION RATES

The collision theory of reaction rates in its simplest form (the “simple collision theory”
or SCT) is one of two theories discussed in this chapter. Collision theories are based on
the notion that only when reactants encounter each other, or collide, do they have the
chance to react. The reaction rate is therefore based on the following expressions:

reaction rate = number of effective collisions m-3s-1 (6.4-1)

or, reaction rate =
(number of collisions m-3 s-l) X (probability of success (energy, orientation, etc.))
(6.4-2)