Page 223 - Introduction to chemical reaction engineering and kinetics

8.5 Heterogeneous Catalysis: Kinetics in Porous Catalyst Particles 205

0.1 1 10 IC
4
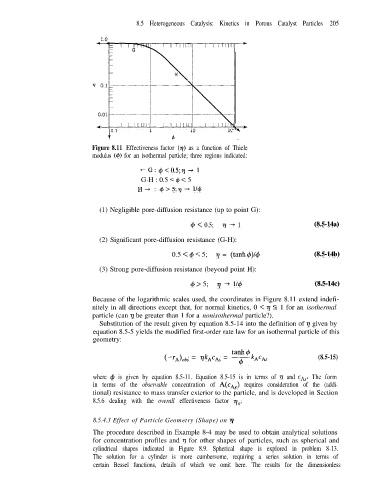
Figure 8.11 Effectiveness factor (n) as a function of Thiele
modulus (4) for an isothermal particle; three regions indicated:

+-G: +<0.5;q + 1
G-H : 0.5 < 4 < 5
H-, : 4>5;r/-+ l/+

(1) Negligible pore-diffusion resistance (up to point G):

cp < 0.5; q + 1 (8.5-14a)
(2) Significant pore-diffusion resistance (G-H):

0.5 < 4 < 5; n = (tanh4)/4 (8.5-14b)

(3) Strong pore-diffusion resistance (beyond point H):

4 > 5; ?j -+ 114 (8.5-14c)
Because of the logarithmic scales used, the coordinates in Figure 8.11 extend indefi-
nitely in all directions except that, for normal kinetics, 0 < 7 5 1 for an isothermal
particle (can n be greater than 1 for a nonisothermal particle?).
Substitution of the result given by equation 8.5-14 into the definition of n given by
equation 8.5-5 yields the modified first-order rate law for an isothermal particle of this
geometry:

(-rA)obs = qkAck, = ykAck, (8.5-15)

where 4 is given by equation 8.5-11. Equation 8.5-15 is in terms of q and cAs. The form
in terms of the observable concentration of A(cAg) requires consideration of the (addi-
tional) resistance to mass transfer exterior to the particle, and is developed in Section
8.5.6 dealing with the overall effectiveness factor no.

8.5.4.3 Effect of Particle Geometry (Shape) on T,J
The procedure described in Example 8-4 may be used to obtain analytical solutions
for concentration profiles and q for other shapes of particles, such as spherical and
cylindrical shapes indicated in Figure 8.9. Spherical shape is explored in problem 8-13.
The solution for a cylinder is more cumbersome, requiring a series solution in terms of
certain Bessel functions, details of which we omit here. The results for the dimensionless