Page 224 - Introduction to chemical reaction engineering and kinetics

206 Chapter 8: Catalysis and Catalytic Reactions

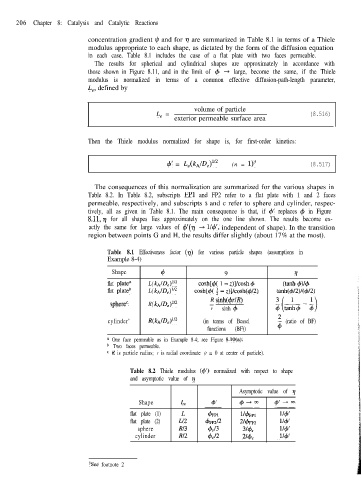
concentration gradient Cc, and for 77 are summarized in Table 8.1 in terms of a Thiele
modulus appropriate to each shape, as dictated by the form of the diffusion equation
in each case. Table 8.1 includes the case of a flat plate with two faces permeable.
The results for spherical and cylindrical shapes are approximately in accordance with
those shown in Figure 8.11, and in the limit of 4 + large, become the same, if the Thiele
modulus is normalized in terms of a common effective diffusion-path-length parameter,
L,, defined by

volume of particle
L, = (8.516)
exterior permeable surface area

Then the Thiele modulus normalized for shape is, for first-order kinetics:

4’ = L,(k/JD,)‘” (n = 1)3 (8.517)

The consequences of this normalization are summarized for the various shapes in
Table 8.2. In Table 8.2, subscripts FPl and FP2 refer to a flat plate with 1 and 2 faces
permeable, respectively, and subscripts s and c refer to sphere and cylinder, respec-
tively, all as given in Table 8.1. The main consequence is that, if 4’ replaces 4 in Figure
8.11,7 for all shapes lies approximately on the one line shown. The results become ex-
actly the same for large values of $‘(q + l/+‘, independent of shape). In the transition
region between points G and H, the results differ slightly (about 17% at the most).

Table 8.1 Effectiveness factor (7) for various particle shapes (assumptions in
Example 8-4)
Shape 4 9 rl

flat platea L( k*ID,)‘” cosh[4( 1 - z)]/cosh 4 (tanh 4114
flat plateb L( kAID,)1’2 cosh[+( $ - z)]/cosh(+/2) tanh(@2)/(+/2)
R sinh(@/R)
sphereC R( kA/D,)‘/2 -
r sinh C#J g&&J
cylinder’ R(kA/D,)“2 (in terms of Bessel 3 (ratio of BF)
functions (BF))
a One face permeable as in Example 8-4; see Figure 8.10(a).
b Two faces permeable.
c R is particle radius; r is radial coordinate (r = 0 at center of particle).

Table 8.2 Thiele modulus (4’) normalized with respect to shape
and asymptotic value of v

Asymptotic value of 77
Shape -L
flat plate (1) L
flat plate (2) Ll2
sphere RI3
cylinder RI2

3See footnote 2