Page 220 - Introduction to chemical reaction engineering and kinetics

202 Chapter 8: Catalysis and Catalytic Reactions

Permeable
f a c e 1
Impermeable
faces

A@) -

- dx

i
l
(a)

0
0 0.5 1
z=.dL
(b)
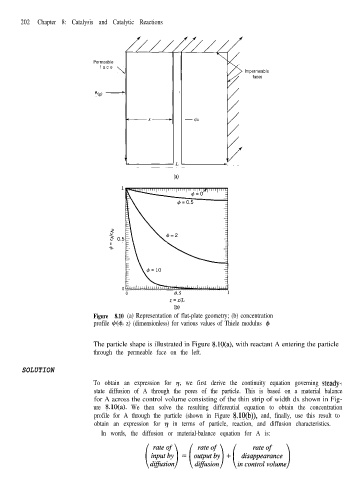
Figure 8.10 (a) Representation of flat-plate geometry; (b) concentration
profile +!J(+, z) (dimensionless) for various values of Thiele modulus 4

The particle shape is illustrated in Figure &lo(a), with reactant A entering the particle
through the permeable face on the left.

SOLUTION

To obtain an expression for q, we first derive the continuity equation governing steady-
state diffusion of A through the pores of the particle. This is based on a material balance
for A across the control volume consisting of the thin strip of width dx shown in Fig-
ure 8.10(a). We then solve the resulting differential equation to obtain the concentration
profile for A through the particle (shown in Figure &lo(b)), and, finally, use this result to
obtain an expression for 77 in terms of particle, reaction, and diffusion characteristics.
In words, the diffusion or material-balance equation for A is: