Page 149 - Materials Chemistry, Second Edition

7.2 Methods 145

w2
w2
min
min
w3 ≥ w3 w1 ≥ w1
min
w2 ≥ w2
max
w1 ≤ w1
max
w3 ≤ w3
W W
max
w2 ≤ w2
w1 w1
w3
w3
(A) (B)
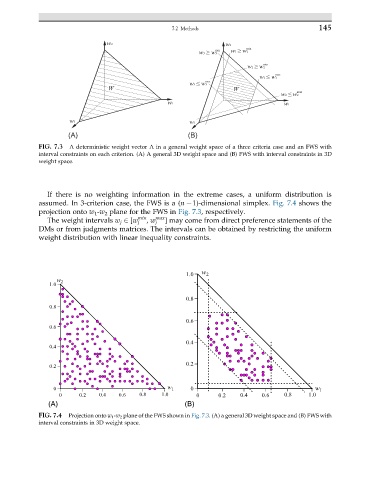
FIG. 7.3 A deterministic weight vector A in a general weight space of a three criteria case and an FWS with
interval constraints on each criterion. (A) A general 3D weight space and (B) FWS with interval constraints in 3D
weight space.

If there is no weighting information in the extreme cases, a uniform distribution is
assumed. In 3-criterion case, the FWS is a (n 1)-dimensional simplex. Fig. 7.4 shows the
projection onto w 1 -w 2 plane for the FWS in Fig. 7.3, respectively.
min max
The weight intervals w j 2 [w j , w j ] may come from direct preference statements of the
DMs or from judgments matrices. The intervals can be obtained by restricting the uniform
weight distribution with linear inequality constraints.

1.0 w 2
w 2
1.0
0.8
0.8
0.6
0.6

0.4
0.4

0.2
0.2

0 w 1 0 w 1
0 0.2 0.4 0.6 0.8 1.0 0 0.2 0.4 0.6 0.8 1.0
(A) (B)
FIG. 7.4 Projection onto w 1 -w 2 plane of the FWS shown in Fig. 7.3. (A) a general 3D weight space and (B) FWS with
interval constraints in 3D weight space.