Page 169 - Lindens Handbook of Batteries

6.22 PRINCIPLES OF OPERATION

the values for the parameters used in the model. The number of parameters used in a physics-based
model is considerably higher than an empirical fit. While most of these parameters are available
from the operating conditions and the design of the cell components at the initial cycle, monitor-
ing changes in several parameters over several cycles is not straightforward. Also, changes in many
parameters depend on the operating conditions or the history of the battery.
The simplest life prediction models use linear extrapolation: plotting the capacity of the cell
versus the cycle number and obtaining the slope and the intercept of a straight line by regression.
When a cell is subjected to repeated cycling under mild operating conditions (e.g., shallow depths
of discharge) that do not cause severe wear out of the cell until the end of life criterion is reached,
linear extrapolation has been found to provide a good degree of confidence in predicting the end
of life of the cell. The primary advantage of using this technique is the ease of extracting the coef-
ficients. Depending on the range of operating conditions, more than one set of coefficients may be
required for successful prediction of the cell performance. For example, if several cells are subject to
different depths of discharge (DOD) at the end of each cycle, the degradation rates are different—and
consequently, the coefficients in the empirical fits for each case are different. Some predictions made
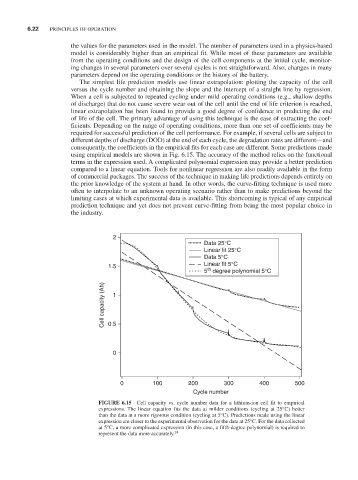
using empirical models are shown in Fig. 6.15. The accuracy of the method relies on the functional
terms in the expression used. A complicated polynomial expression may provide a better prediction
compared to a linear equation. Tools for nonlinear regression are also readily available in the form
of commercial packages. The success of the technique in making life predictions depends entirely on
the prior knowledge of the system at hand. In other words, the curve-fitting technique is used more
often to interpolate to an unknown operating scenario rather than to make predictions beyond the
limiting cases at which experimental data is available. This shortcoming is typical of any empirical
prediction technique and yet does not prevent curve-fitting from being the most popular choice in
the industry.

2
Data 25°C
Linear fit 25°C
Data 5°C
1.5 Linear fit 5°C
th
5 degree polynomial 5°C
Cell capacity (Ah) 0.5 1

0

0 100 200 300 400 500
Cycle number
FiguRE 6.15 Cell capacity vs. cycle number data for a lithium-ion cell fit to empirical
expressions. The linear equation fits the data at milder conditions (cycling at 25°C) better
than the data at a more rigorous condition (cycling at 5°C). Predictions made using the linear
expression are closer to the experimental observation for the data at 25°C. For the data collected
at 5°C, a more complicated expression (in this case, a fifth-degree polynomial) is required to
represent the data more accurately. 24