Page 170 - Lindens Handbook of Batteries

MATHEMATICAL MODELING OF BATTERIES 6.23

TABLE 6.4 Summary of equations used to represent a porous intercalation electrode. The corresponding
equation numbers from the text are shown in the last column. 18
Equation
number in
Variable Governing equation the text
Solid phase potential (φ , 1 j ) i =- σ eff j ∇ φ 1, j (6.12)
1
0 ∇
- (
c 
Solution phase potential (φ , 2 j ) i =- κ eff    ∇ 2 +φ 2 RT 12 t ) c   (6.45)
2
+
F
i
Solid phase current density (i ) i tot =+ i (6.44)
1
2
1
nFη
n Fη
di 2  α aj j s j   -α c j j j s j  
,
,
,
,
Solution phase current density (i ) dx = ia exp   RT   - exp   RT    (6.40)
j 
0,

2

2
∂c s  ∂ c s 2 ∂ 
c
s
s
Solid phase concentration (c ) = D s  2 +  (6.46)
∂t  ∂r r r
∂ 
2
∂c ∂ c 1 ( - + t ) ∂i 2
Solution phase concentration (c ) ε ∂t = D eff ∂x 2 + F ∂x (6.38)
2
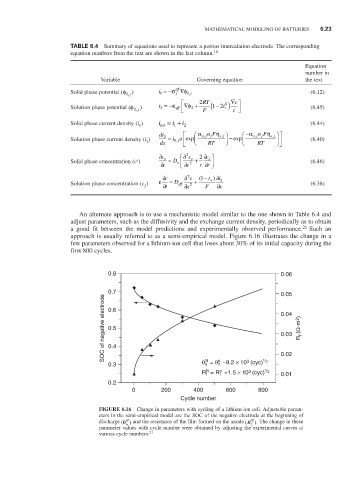
An alternate approach is to use a mechanistic model similar to the one shown in Table 6.4 and
adjust parameters, such as the diffusivity and the exchange current density, periodically as to obtain
a good fit between the model predictions and experimentally observed performance. 21 Such an
approach is usually referred to as a semi-empirical model. Figure 6.16 illustrates the change in a
few parameters observed for a lithium-ion cell that loses about 30% of its initial capacity during the
first 800 cycles.
0.8 0.06
0.7 0.05
SOC of negative electrode 0.5 0.04 R f (Ω-m 2 )
0.6
0.03
0.4
o
N
3
n
n
0.3 θ = θ –9.2 × 10 (cyc) 1 / 2 0.02
o
N
3
R = R +1.5 × 10 (cyc) 1 / 2 0.01
f
f
0.2
0 200 400 600 800
Cycle number
FiguRE 6.16 Change in parameters with cycling of a lithium-ion cell. Adjustable param-
eters in the semi-empirical model are the SOC of the negative electrode at the beginning of
N N
discharge (θ n ) and the resistance of the film formed on the anode (R f ). The change in these
parameter values with cycle number were obtained by adjusting the experimental curves at
21
various cycle numbers.