Page 171 - Lindens Handbook of Batteries

6.24 PRINCIPLES OF OPERATION

A third approach is the development of a mechanistic model for the degradation process.
An electrochemical reaction that consumes part of the cell’s deliverable capacity over several
N
cycles may be proposed. For example, the increase in resistance R is modeled as a film formed
f
22
on the surface of the anode particles due to reduction of the solvent during charge. Since this
+
is a charge transfer reaction involving reduction of Li into salts, a Butler-Volmer type equation
assumes the following form:
n
di side  α asideside Fη side  
,
dx =- i 0, side aexp   -  RT  (6.53)
 
The formation of the film introduces an additional resistance at the surface of the anode particles
and consequently a drop in the overpotential at the anode
 
η φ = - φ - E - 1    i ∂ 2   δ film  
 
n 1, s 2, s n a n  x ∂   κ film   
  (6.54)
1  ∂i  δ
=η - φ - φ - E  side   fiilm 
side 1, s 2, s side a  ∂x   

n   κ film 
The thickness of the film δ film is calculated knowing the amount of capacity lost, using Faraday’s law
∂δ 1  ∂i   M 
film =-  side   side   (6.55)
∂t Fa n  ∂   ρ side 
x
where M side and ρ side represent the molecular weight of the side reaction product and the density of
the film, respectively.
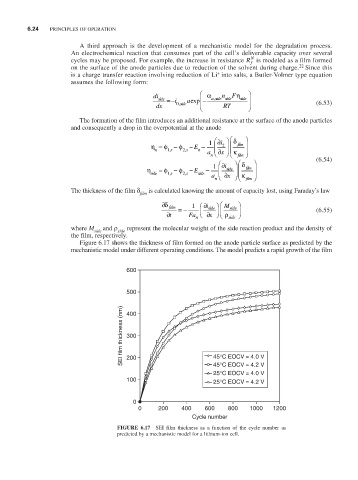
Figure 6.17 shows the thickness of film formed on the anode particle surface as predicted by the
mechanistic model under different operating conditions. The model predicts a rapid growth of the film

600

500

SEI film thickness (nm) 300
400

45°C EOCV = 4.0 V
200
45°C EOCV = 4.2 V
25°C EOCV = 4.0 V
100 25°C EOCV = 4.2 V

0
0 200 400 600 800 1000 1200
Cycle number
FiguRE 6.17 SEI film thickness as a function of the cycle number as
predicted by a mechanistic model for a lithium-ion cell.