Page 253 - MATLAB an introduction with applications
P. 253
238 ——— MATLAB: An Introduction with Applications
0.14
0.12
0.1
error 0.08
Normalized 0.06
0.04
0.02
0
1 2 3 4 5 6 7 8 9
Iteration #
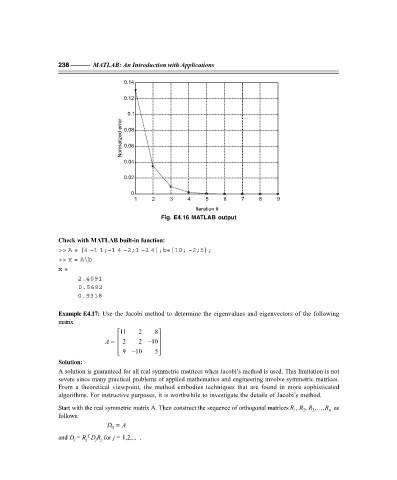
Fig. E4.16 MATLAB output
Check with MATLAB built-in function:
>> A = [4 –1 1;–1 4 –2;1 –2 4];b=[10; –2;5];
>> x = A\b
x =
2.4091
0.5682
0.9318
Example E4.17: Use the Jacobi method to determine the eigenvalues and eigenvectors of the following
matrix
11 2 8
A = 2 2 –10
9 –10 5
Solution:
A solution is guaranteed for all real symmetric matrices when Jacobi’s method is used. This limitation is not
severe since many practical problems of applied mathematics and engineering involve symmetric matrices.
From a theoretical viewpoint, the method embodies techniques that are found in more sophisticated
algorithms. For instructive purposes, it is worthwhile to investigate the details of Jacobi’s method.
Start with the real symmetric matrix A. Then construct the sequence of orthogonal matrices R , R , R ,…,R as
3
n
1
2
follows:
D = A
0
T
and D = R D R for j = 1,2,... .
j
j j
j