Page 326 - MATLAB an introduction with applications

Optimization ——— 311

2
2
Example E5.28: Find the minimum of the function f(X) = 4x + 3x – 5x x – 8x starting from (0, 0) using
1 2
1
2
1
Powell’s method
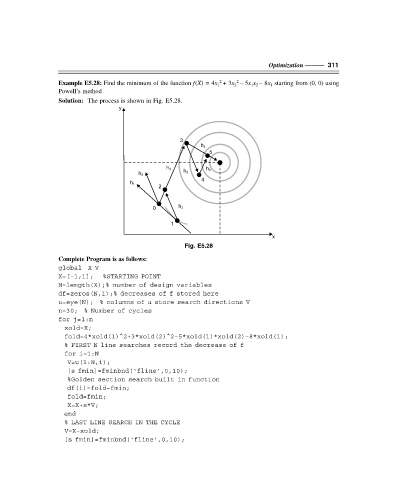
Solution: The process is shown in Fig. E5.28.
y

3
h 4
5

h 3
h 3
h 2
h 2
4
h 1
2
0 h 2

1
x
Fig. E5.28
Complete Program is as follows:
global X V
X=[–1;1]; %STARTING POINT
N=length(X);% number of design variables
df=zeros(N,1);% decreases of f stored here
u=eye(N); % columns of u store search directions V
n=30; % Number of cycles
for j=1:n
xold=X;
fold=4*xold(1)^2+3*xold(2)^2–5*xold(1)*xold(2)–8*xold(1);
% FIRST N line searches record the decrease of f
for i=1:N
V=u(1:N,i);
[s fmin]=fminbnd(‘fline’,0,10);
%Golden section search built in function
df(i)=fold–fmin;
fold=fmin;
X=X+s*V;
end
% LAST LINE SEARCH IN THE CYCLE
V=X–xold;
[s fmin]=fminbnd(‘fline’,0,10);