Page 216 - Master Handbook of Acoustics

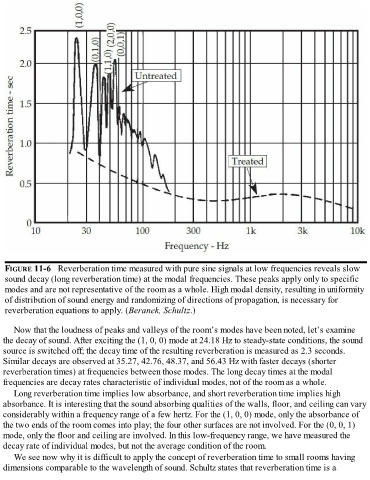
FIGURE 11-6 Reverberation time measured with pure sine signals at low frequencies reveals slow
sound decay (long reverberation time) at the modal frequencies. These peaks apply only to specific
modes and are not representative of the room as a whole. High modal density, resulting in uniformity
of distribution of sound energy and randomizing of directions of propagation, is necessary for
reverberation equations to apply. (Beranek, Schultz.)

Now that the loudness of peaks and valleys of the room’s modes have been noted, let’s examine

the decay of sound. After exciting the (1, 0, 0) mode at 24.18 Hz to steady-state conditions, the sound
source is switched off; the decay time of the resulting reverberation is measured as 2.3 seconds.
Similar decays are observed at 35.27, 42.76, 48.37, and 56.43 Hz with faster decays (shorter
reverberation times) at frequencies between those modes. The long decay times at the modal
frequencies are decay rates characteristic of individual modes, not of the room as a whole.
Long reverberation time implies low absorbance, and short reverberation time implies high

absorbance. It is interesting that the sound absorbing qualities of the walls, floor, and ceiling can vary
considerably within a frequency range of a few hertz. For the (1, 0, 0) mode, only the absorbance of
the two ends of the room comes into play; the four other surfaces are not involved. For the (0, 0, 1)
mode, only the floor and ceiling are involved. In this low-frequency range, we have measured the
decay rate of individual modes, but not the average condition of the room.

We see now why it is difficult to apply the concept of reverberation time to small rooms having
dimensions comparable to the wavelength of sound. Schultz states that reverberation time is a