Page 217 - Master Handbook of Acoustics
P. 217
statistical concept “in which much of the mathematically awkward details are averaged out.” In small
rooms these details are not averaged out.
The reverberation-time equations of Sabine, Eyring-Norris, and others are based on the
assumption of an enclosed space with a highly uniform distribution of sound energy and random
direction of propagation of sound. At low frequencies in the room presented in Fig. 11-6, energy is
distributed very unevenly and direction of propagation is far from random. After the room is treated,
reverberation time measurements would follow the broken line, but statistical randomness still does
not prevail below 200 Hz even though modal frequencies are brought under some measure of control.
Analysis of Decay Traces
An octave band of pink noise viewed on an oscilloscope shows a trace that looks very much like a
sine wave, except that it is constantly shifting in amplitude and phase, because of the random property
of noise. This characteristic of random noise has its effect on the shape of the reverberatory decay
trace. Consider what this constantly shifting random noise signal does to the normal modes of a room.
When the axial, tangential, and oblique resonant modes are considered, they are quite close together
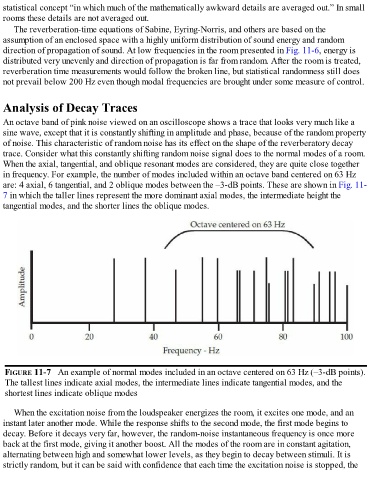
in frequency. For example, the number of modes included within an octave band centered on 63 Hz
are: 4 axial, 6 tangential, and 2 oblique modes between the –3-dB points. These are shown in Fig. 11-
7 in which the taller lines represent the more dominant axial modes, the intermediate height the
tangential modes, and the shorter lines the oblique modes.
FIGURE 11-7 An example of normal modes included in an octave centered on 63 Hz (–3-dB points).
The tallest lines indicate axial modes, the intermediate lines indicate tangential modes, and the
shortest lines indicate oblique modes
When the excitation noise from the loudspeaker energizes the room, it excites one mode, and an
instant later another mode. While the response shifts to the second mode, the first mode begins to
decay. Before it decays very far, however, the random-noise instantaneous frequency is once more
back at the first mode, giving it another boost. All the modes of the room are in constant agitation,
alternating between high and somewhat lower levels, as they begin to decay between stimuli. It is
strictly random, but it can be said with confidence that each time the excitation noise is stopped, the