Page 85 - Materials Science and Engineering An Introduction

3.4 Metallic Crystal Structures • 57

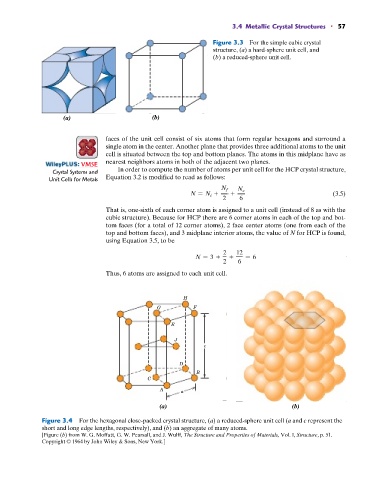
Figure 3.3 For the simple cubic crystal
structure, (a) a hard-sphere unit cell, and
(b) a reduced-sphere unit cell.

(a) (b)

faces of the unit cell consist of six atoms that form regular hexagons and surround a
single atom in the center. Another plane that provides three additional atoms to the unit
cell is situated between the top and bottom planes. The atoms in this midplane have as
nearest neighbors atoms in both of the adjacent two planes.
: VMSE
Crystal Systems and In order to compute the number of atoms per unit cell for the HCP crystal structure,
Unit Cells for Metals Equation 3.2 is modified to read as follows:
N f N c
N = N i + + (3.5)
2 6
That is, one-sixth of each corner atom is assigned to a unit cell (instead of 8 as with the
cubic structure). Because for HCP there are 6 corner atoms in each of the top and bot-
tom faces (for a total of 12 corner atoms), 2 face center atoms (one from each of the
top and bottom faces), and 3 midplane interior atoms, the value of N for HCP is found,
using Equation 3.5, to be

2 12
N = 3 + + = 6
2 6
Thus, 6 atoms are assigned to each unit cell.

H
G F

E

J
c

D
B
C
A a

(a) (b)
Figure 3.4 For the hexagonal close-packed crystal structure, (a) a reduced-sphere unit cell (a and c represent the
short and long edge lengths, respectively), and (b) an aggregate of many atoms.
[Figure (b) from W. G. Moffatt, G. W. Pearsall, and J. Wulff, The Structure and Properties of Materials, Vol. I, Structure, p. 51.
Copyright © 1964 by John Wiley & Sons, New York.]