Page 166 - Mathematical Techniques of Fractional Order Systems

154 Mathematical Techniques of Fractional Order Systems

0.5

0

–0.5

–1

–1.5
0 5 10 15 20 25
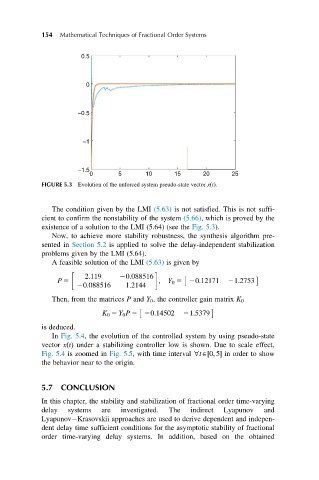
FIGURE 5.3 Evolution of the unforced system pseudo-state vector xðtÞ.

The condition given by the LMI (5.63) is not satisfied. This is not suffi-
cient to confirm the nonstability of the system (5.66), which is proved by the
existence of a solution to the LMI (5.64) (see the Fig. 5.3).
Now, to achieve more stability robustness, the synthesis algorithm pre-
sented in Section 5.2 is applied to solve the delay-independent stabilization
problems given by the LMI (5.64).
A feasible solution of the LMI (5.63) is given by

2:119 20:088516
P 5 ; Y 0 520:12171 21:2753
20:088516 1:2144
Then, from the matrices P and Y 0 , the controller gain matrix K 0

K 0 5 Y 0 P 520:14502 21:5379
is deduced.
In Fig. 5.4, the evolution of the controlled system by using pseudo-state
vector xðtÞ under a stabilizing controller low is shown. Due to scale effect,
Fig. 5.4 is zoomed in Fig. 5.5, with time interval ’tA½0; 5Š in order to show
the behavior near to the origin.

5.7 CONCLUSION
In this chapter, the stability and stabilization of fractional order time-varying
delay systems are investigated. The indirect Lyapunov and
Lyapunov Krasovskii approaches are used to derive dependent and indepen-
dent delay time sufficient conditions for the asymptotic stability of fractional
order time-varying delay systems. In addition, based on the obtained