Page 393 - Mathematical Techniques of Fractional Order Systems

382 Mathematical Techniques of Fractional Order Systems

corresponds to more degrees of freedom required in the coding and commu-
nication applications with asymmetric transmission probabilities of binary
zeros and ones (Sayed et al., 2015a,b).

13.2.2.1 Generalized Logistic Map With Scaling Parameters
The generalized logistic map with scaling parameters (Sayed et al., 2015b)is
given by:
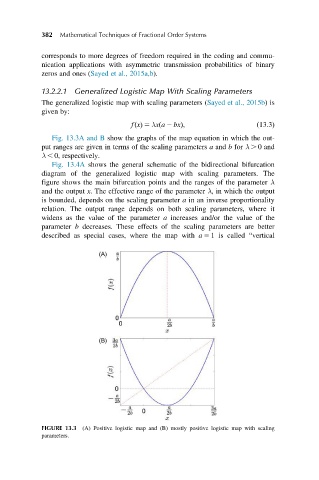
fðxÞ 5 λxða 2 bxÞ; ð13:3Þ

Fig. 13.3A and B show the graphs of the map equation in which the out-
put ranges are given in terms of the scaling parameters a and b for λ . 0 and
λ , 0, respectively.
Fig. 13.4A shows the general schematic of the bidirectional bifurcation
diagram of the generalized logistic map with scaling parameters. The
figure shows the main bifurcation points and the ranges of the parameter λ
and the output x. The effective range of the parameter λ, in which the output
is bounded, depends on the scaling parameter a in an inverse proportionality
relation. The output range depends on both scaling parameters, where it
widens as the value of the parameter a increases and/or the value of the
parameter b decreases. These effects of the scaling parameters are better
described as special cases, where the map with a 5 1 is called “vertical

FIGURE 13.3 (A) Positive logistic map and (B) mostly positive logistic map with scaling
parameters.