Page 395 - Mathematical Techniques of Fractional Order Systems

384 Mathematical Techniques of Fractional Order Systems

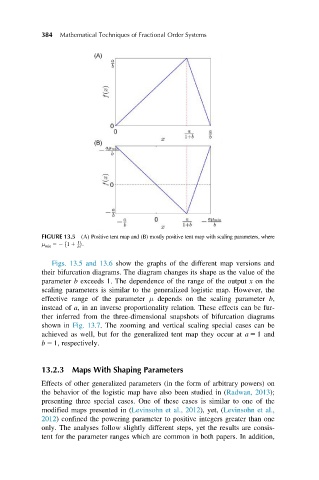
FIGURE 13.5 (A) Positive tent map and (B) mostly positive tent map with scaling parameters, where

μ min 52 1 1 1 .
b
Figs. 13.5 and 13.6 show the graphs of the different map versions and
their bifurcation diagrams. The diagram changes its shape as the value of the
parameter b exceeds 1. The dependence of the range of the output x on the
scaling parameters is similar to the generalized logistic map. However, the
effective range of the parameter μ depends on the scaling parameter b,
instead of a, in an inverse proportionality relation. These effects can be fur-
ther inferred from the three-dimensional snapshots of bifurcation diagrams
shown in Fig. 13.7. The zooming and vertical scaling special cases can be
achieved as well, but for the generalized tent map they occur at a 5 1 and
b 5 1, respectively.

13.2.3 Maps With Shaping Parameters
Effects of other generalized parameters (in the form of arbitrary powers) on
the behavior of the logistic map have also been studied in (Radwan, 2013);
presenting three special cases. One of these cases is similar to one of the
modified maps presented in (Levinsohn et al., 2012), yet, (Levinsohn et al.,
2012) confined the powering parameter to positive integers greater than one
only. The analyses follow slightly different steps, yet the results are consis-
tent for the parameter ranges which are common in both papers. In addition,