Page 399 - Mathematical Techniques of Fractional Order Systems

388 Mathematical Techniques of Fractional Order Systems

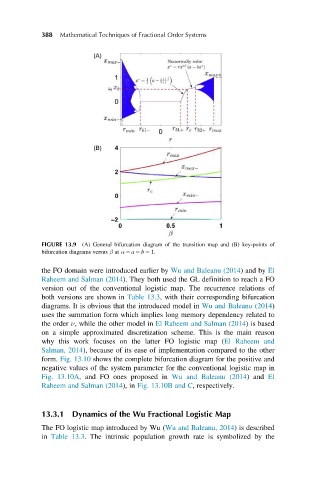
FIGURE 13.9 (A) General bifurcation diagram of the transition map and (B) key-points of
bifurcation diagrams versus β at α 5 a 5 b 5 1.

the FO domain were introduced earlier by Wu and Baleanu (2014) and by El
Raheem and Salman (2014). They both used the GL definition to reach a FO
version out of the conventional logistic map. The recurrence relations of
both versions are shown in Table 13.3, with their corresponding bifurcation
diagrams. It is obvious that the introduced model in Wu and Baleanu (2014)
uses the summation form which implies long memory dependency related to
the order ν, while the other model in El Raheem and Salman (2014) is based
on a simple approximated discretization scheme. This is the main reason
why this work focuses on the latter FO logistic map (El Raheem and
Salman, 2014), because of its ease of implementation compared to the other
form. Fig. 13.10 shows the complete bifurcation diagram for the positive and
negative values of the system parameter for the conventional logistic map in
Fig. 13.10A, and FO ones proposed in Wu and Baleanu (2014) and El
Raheem and Salman (2014), in Fig. 13.10B and C, respectively.

13.3.1 Dynamics of the Wu Fractional Logistic Map

The FO logistic map introduced by Wu (Wu and Baleanu, 2014) is described
in Table 13.3. The intrinsic population growth rate is symbolized by the