Page 402 - Mathematical Techniques of Fractional Order Systems
P. 402
On the Fractional Order Generalized Discrete Maps Chapter | 13 391
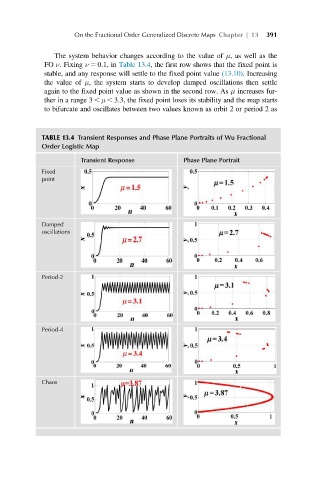
The system behavior changes according to the value of μ,aswellasthe
FO ν.Fixing ν 5 0:1, in Table 13.4, the first row shows that the fixed point is
stable, and any response will settle to the fixed point value (13.10).Increasing
the value of μ, the system starts to develop damped oscillations then settle
again to the fixed point value as shown in the second row. As μ increases fur-
ther in a range 3 , μ , 3:3, the fixed point loses its stability and the map starts
to bifurcate and oscillates between two values known as orbit 2 or period 2 as
TABLE 13.4 Transient Responses and Phase Plane Portraits of Wu Fractional
Order Logistic Map
Transient Response Phase Plane Portrait
Fixed
point
Damped
oscillations
Period-2
Period-4
Chaos